题目内容
已知数列{an}是等差数列,a2=3,a5=6,数列{bn}的前n项和是Tn,且Tn+ bn=1.
bn=1.(1)求数列{an}的通项公式与前n项的和Mn.(2)求数列{bn}的通项公式.
【答案】分析:(1)设{an}的公差为d,进而根据等差数列通项公式表示出a2和a5,求得a1和d,则数列的通项公式和求和公式可得.
(2)根据Tn-Tn-1=bn,整理得bn= bn-1.判断出{bn}是等比数列.进而求得b1,利用等比数列的通项公式求得答案.
bn-1.判断出{bn}是等比数列.进而求得b1,利用等比数列的通项公式求得答案.
解答:解:(1)设{an}的公差为d,则:a2=a1+d,a5=a1+4d.∴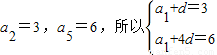 ,
,
∴a1=2,d=1
∴an=2+(n-1)=n+1.
Mn=na1+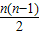 d=
d=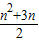 .
.
(2)当n=1时,b1=T1,
由T1+ b1=1,得b1=
b1=1,得b1= .
.
当n≥2时,∵Tn=1- bn,Tn-1=1-
bn,Tn-1=1- bn-1,
bn-1,
∴Tn-Tn-1= (bn-1-bn),
(bn-1-bn),
即bn= (bn-1-bn).
(bn-1-bn).
∴bn= bn-1.
bn-1.
∴{bn}是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
∴bn= •(
•( )n-1=
)n-1=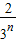 .
.
点评:本题主要考查了等差数列的性质和等比数列的判定.考查了学生对数列基本知识点的掌握.
(2)根据Tn-Tn-1=bn,整理得bn=
 bn-1.判断出{bn}是等比数列.进而求得b1,利用等比数列的通项公式求得答案.
bn-1.判断出{bn}是等比数列.进而求得b1,利用等比数列的通项公式求得答案.解答:解:(1)设{an}的公差为d,则:a2=a1+d,a5=a1+4d.∴
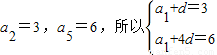 ,
,∴a1=2,d=1
∴an=2+(n-1)=n+1.
Mn=na1+
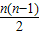 d=
d=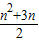 .
.(2)当n=1时,b1=T1,
由T1+
 b1=1,得b1=
b1=1,得b1= .
.当n≥2时,∵Tn=1-
 bn,Tn-1=1-
bn,Tn-1=1- bn-1,
bn-1,∴Tn-Tn-1=
 (bn-1-bn),
(bn-1-bn),即bn=
 (bn-1-bn).
(bn-1-bn).∴bn=
 bn-1.
bn-1.∴{bn}是以
 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.∴bn=
 •(
•( )n-1=
)n-1=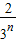 .
.点评:本题主要考查了等差数列的性质和等比数列的判定.考查了学生对数列基本知识点的掌握.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目