题目内容
设椭圆
分析:主要考虑利用椭圆的定义、离心率的概念以及函数与方程思想来解决.
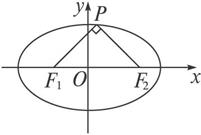
解:解法一:如右图所示
设F1(-c,0),F2(c,0),P(x0,y0),
则|PF1|=a+ex0,
|PF2|=a-ex0,|F1F2|=2c
∵![]() ·
·![]() =0,∴
=0,∴![]() ⊥
⊥![]() ,
,
∴|PF1|2+|PF2|2=|F1F2|2,
即(a+ex0)2+(a-ex0)2=4c2![]() e2x02=2c2-a2,据题意,P点在椭圆上,但不在x轴上,∴0≤x02<a2,∴0≤e2x02<c2,
e2x02=2c2-a2,据题意,P点在椭圆上,但不在x轴上,∴0≤x02<a2,∴0≤e2x02<c2,
于是0≤2c2-a2<c2,即![]() ≤c2<a2
≤c2<a2![]()
![]() ≥
≥![]() ,
,![]() <1,∴e∈[
<1,∴e∈[![]() ,1).
,1).
解法二:∵![]() ·
·![]() =0,∴
=0,∴![]() ⊥
⊥![]() ,
,
∴P点在以F1F2为直径的圆上,又P点在椭圆上,
∴圆x2+y2=c2与椭圆![]() =1有公共点,
=1有公共点,
由图知,b≤c<a![]() b2≤c2<a2,即a2-c2≤c2<a2,
b2≤c2<a2,即a2-c2≤c2<a2,
∴![]() ≤c2<a2
≤c2<a2![]()
![]() ≤
≤![]() <1,∴e∈[
<1,∴e∈[![]() ,1).
,1).
点拨:对于条件![]() ·
·![]() =0,即
=0,即![]() ⊥
⊥![]() 可作多种变化,本题也可以改为“当∠F1PF2为某锐角或钝角时,求离心率e的取值范围.”
可作多种变化,本题也可以改为“当∠F1PF2为某锐角或钝角时,求离心率e的取值范围.”

练习册系列答案
相关题目
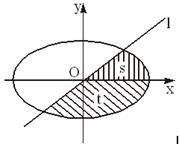













 +
+ =1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.
=1(a>b>0)的左焦点为F1(-2,0),左准线l1与x轴交于点N(-3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.