题目内容

定义在R上的函数f（x）满足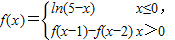则f（27）=    ．
【答案】分析：利用分段函数在不同区间上的解析式不同即可求出函数值．
解答：解：∵27＞0，∴f（27）=f（26）-f（25）=f（25）-f（24）-f（25）=-f（24）
=-[f（23）-f（22）]=-[f（22）-f（21）-f（22）]=f（21）=f（3×6+3）
=f（3）=f（2）-f（1）=f（1）-f（0）-f（1）=-f（0），
∵0≤0，∴f（0）=ln5．
∴f（27）=-f（0）=-ln5．
故答案为-ln5．
点评：正确理解分段函数的意义是解题的关键．
练习册系列答案
相关题目
定义在R上的函数f（x）既是偶函数又是周期函数，若f（x）的最小正周期是π，且当x∈[0，
π
2
]时，f（x）=sinx，则f（
5π
3
）的值为
 
．
20、已知定义在R上的函数f（x）=-2x3+bx2+cx（b，c∈R），函数F（x）=f（x）-3x2是奇函数，函数f（x）在x=-1处取极值．
（1）求f（x）的解析式；
（2）讨论f（x）在区间[-3，3]上的单调性．
定义在R上的函数f（x）满足：f(x+2)=
1-f(x)1+f(x)
，当x∈（0，4）时，f（x）=x2-1，则f（2010）=
 
．
已知定义在R上的函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，|φ|≤
π
2
），最大值与最小值的差为4，相邻两个最低点之间距离为π，函数y=sin（2x+
π
3
）图象所有对称中心都在f（x）图象的对称轴上．
（1）求f（x）的表达式；    
（2）若f（
x0
2
）=
3
2
（x0∈[-
π
2
，
π
2
]），求cos（x0-
π
3
）的值．
已知定义在R上的函数f（x）的图象是连续不断的，且有如下对应值表：
x 0 1 2 3
f（x） 3.1 0.1 -0.9 -3
那么函数f（x）一定存在零点的区间是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网