题目内容
下列函数中，在（0，2）上为增函数的是（ ）
A．y=log (x+1) | B．y=log2 |
C．y=log2 | D．y=log(x2-4x+5) |
D
解析试题分析：因为选项A, y=log(x+1) ,内层是递增的，外层是递减的，那么复合函数只有减区间，不成立，选项B中，有函数定义域可知
,
那么显然定义域不符。选项C中，由于内层是递减的反比例函数，外层是递增的对数函数，故复合函数递减，排除法选D.
考点：本题主要考查了函数单调性的判定问题的运用。
点评：解决该试题的关键是利用对数函数的单调性，以及复合函数单调性的判定：同增异减的思想来得到判定，注意定义域，是个易错题。
练习册系列答案
相关题目
与
在同一坐标系中的图像只可能是
函数
在区间
上的最大值与最小值的和为3，则
等于（ ）
A． | B．4 | C．2 | D． |
函数
的图象必过定点（ ）
A． | B． | C． | D． |
已知
上是增函数，那么实数a的取值范围是
（ ）
A．（1，+ ） | B．（ ） | C． | D．（1，3） |
下列幂函数中过点
，
的偶函数是 ( )
A． | B． | C． | D． |
已知函数 ，
若
f(a) = 3 ，则a的取值为（ ）
| A．0 | B． | C． | D．1 |
函数
在[0，1]上是
的减函数，则
的取值范围是（ ）
| A．（0，1） | B．（0，2） | C．（1，2） | D．[2，+ ) |
如果函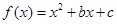数
对任意实数
都有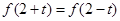
，那么（ ）
A． < < | B．<< |
| C．<< | D．<< |