题目内容
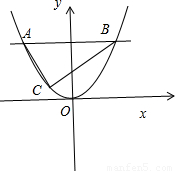
已知直线y=a交抛物线y=x2于A,B两点,若该抛物线上存在点C,使得∠ACB为直角,则a的取值范围为 .
【答案】分析:如图所示,可知A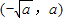 ,B
,B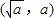 ,设C(m,m2),由该抛物线上存在点C,使得∠ACB为直角,可得
,设C(m,m2),由该抛物线上存在点C,使得∠ACB为直角,可得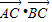 =0.即可得到a的取值范围.
=0.即可得到a的取值范围.
解答:解:如图所示,可知A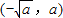 ,B
,B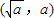 ,
,
设C(m,m2),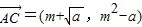 ,
,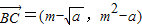 .
.
∵该抛物线上存在点C,使得∠ACB为直角,
∴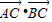 =
=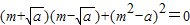 .
.
化为m2-a+(m2-a)2=0.
∵m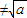 ,∴m2=a-1≥0,解得a≥1.
,∴m2=a-1≥0,解得a≥1.
∴a 的取值范围为[1,+∞).
故答案为[1,+∞).
点评:本题考查了如何表示抛物线上点的坐标、垂直于数量积得关系等基础知识,考查了推理能力和计算能力.
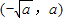 ,B
,B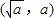 ,设C(m,m2),由该抛物线上存在点C,使得∠ACB为直角,可得
,设C(m,m2),由该抛物线上存在点C,使得∠ACB为直角,可得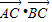 =0.即可得到a的取值范围.
=0.即可得到a的取值范围.解答:解:如图所示,可知A
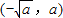 ,B
,B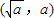 ,
,
设C(m,m2),
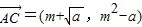 ,
,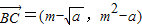 .
.∵该抛物线上存在点C,使得∠ACB为直角,
∴
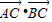 =
=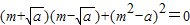 .
.化为m2-a+(m2-a)2=0.
∵m
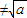 ,∴m2=a-1≥0,解得a≥1.
,∴m2=a-1≥0,解得a≥1.∴a 的取值范围为[1,+∞).
故答案为[1,+∞).
点评:本题考查了如何表示抛物线上点的坐标、垂直于数量积得关系等基础知识,考查了推理能力和计算能力.

练习册系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆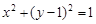 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求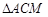 与
与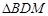 面积之和的最小值.
面积之和的最小值.
(本小题满分15分)
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5。
(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆![]() 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明![]() 为定值;
为定值;
|
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 焦点到渐近线的距离为
焦点到渐近线的距离为
