题目内容
已知函数y= 的定义域为M,集合N={x|y=lg(x-1)∈R,则M∩N=
的定义域为M,集合N={x|y=lg(x-1)∈R,则M∩N=
- A.[0,2)
- B.(0,2)
- C.[1,2)
- D.(1,2]
D
分析:分别由函数所满足的条件求出集合M、N,在进行集合运算即可
解答:∵2-x≥0
∴x≤2
∴M={x|x≤2}
又∵x-1>0
∴x>1
∴N={x|x>1}
∴M∩N={x|1<x≤2}
故选D
点评:本题考查函数定义域的求法和集合运算.求函数定义域时,须把保证函数有意义的条件全部列出,求解不等式(组);集合运算可借助数轴完成.属简单题
分析:分别由函数所满足的条件求出集合M、N,在进行集合运算即可
解答:∵2-x≥0
∴x≤2
∴M={x|x≤2}
又∵x-1>0
∴x>1
∴N={x|x>1}
∴M∩N={x|1<x≤2}
故选D
点评:本题考查函数定义域的求法和集合运算.求函数定义域时,须把保证函数有意义的条件全部列出,求解不等式(组);集合运算可借助数轴完成.属简单题

练习册系列答案
相关题目
 的定义域是A,函数y=
的定义域是A,函数y=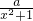 (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围. 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围. 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.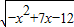 的定义域是A,函数y=
的定义域是A,函数y= (a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.
(a>0)在[0,2]上的值域为B.若A⊆B,求实数a的取值范围.