题目内容
当曲线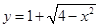
 与直线
与直线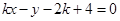 有两个相异的交点时,实数k的取值范围是( )
有两个相异的交点时,实数k的取值范围是( )
A.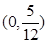 | B.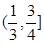 | C.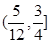 | D.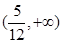 |
C
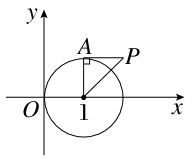
解析试题分析:注意到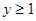 ,知曲线
,知曲线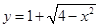 是圆
是圆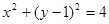 在直线y=1的上方部分的半圆;而直线
在直线y=1的上方部分的半圆;而直线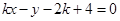
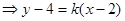 知恒过定点A(2,4),如图:,由于B(-2,1),
知恒过定点A(2,4),如图:,由于B(-2,1),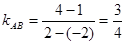 ,当直线与圆相切时:
,当直线与圆相切时: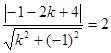 解得
解得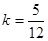 ,故知实数k的取值范围是
,故知实数k的取值范围是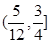
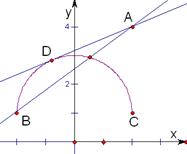
考点:1.直线和圆的位置关系;2.数形结合法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5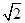 -4 -4 | B.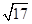 -1 -1 | C.6-2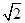 | D.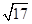 |
若圆的方程为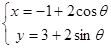 (
( 为参数),直线的方程为
为参数),直线的方程为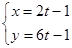 (t为参数),
(t为参数),
则直线与圆的位置关系是( )
| A.相交过圆心 | B.相交而不过圆心 | C.相切 | D.相离 |
直线x-y+m=0与圆x2+y2-2x-1=0有两个不同的交点的一个充分不必要条件为( ).
| A.m<1 | B.-3<m<1 | C.-4<m<2 | D.0<m<1 |
过原点且倾斜角为 的直线被圆学
的直线被圆学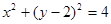 所截得的弦长为(科网 )
所截得的弦长为(科网 )
A.2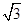 | B.2 | C.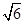 | D.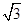 |
两圆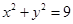 和
和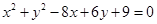 的位置关系是( )
的位置关系是( )
| A.相离 | B.相交 | C.内切 | D.外切 |
 ,动点
,动点 在直线
在直线 上运动,当线段
上运动,当线段 最短时,求
最短时,求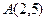 ,
,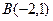 ,
,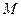 (在第一象限)和
(在第一象限)和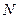 是过原点的直线
是过原点的直线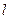 上的两个动点,且
上的两个动点,且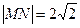 ,
,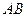 ,如果直线
,如果直线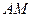 和
和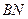 的交点
的交点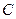 在
在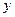 轴上,求点
轴上,求点