题目内容
已知二次函数f(x)开口向上,且对?x∈R都有f(1-x)=f(1+x)成立,设向量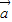 =(x,2),
=(x,2),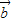 =(2,
=(2, ),
),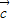 =(1-x,1),
=(1-x,1),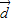 =(1,2);求不等式f>f的解集.
=(1,2);求不等式f>f的解集.
【答案】分析:利用已知条件求出函数的对称轴,求出两个数量积,转化不等式为代数不等式,求出不等式的解集.
解答:解:因为f(1-x)=f(1+x),所以由x的任意性得f(x)的图象关于直线x=1对称,…(2分)
∵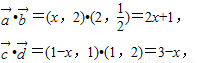 …(6分)
…(6分)
f(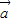 •
•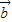 )>f(
)>f(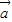 •
•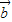 )?f(2x+1)>f(3-x)?|2x|>|2-x|(10分)
)?f(2x+1)>f(3-x)?|2x|>|2-x|(10分)
解得,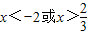 (14分)
(14分)
综上:f(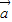 •
•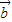 )>f(
)>f(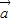 •
•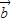 )的解集为
)的解集为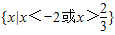 .
.
点评:本题考查不等式的解集的求法,转化思想的应用,向量数量积的应用,考查计算能力.
解答:解:因为f(1-x)=f(1+x),所以由x的任意性得f(x)的图象关于直线x=1对称,…(2分)
∵
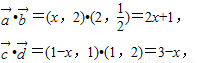 …(6分)
…(6分)f(
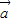 •
•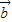 )>f(
)>f(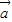 •
•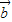 )?f(2x+1)>f(3-x)?|2x|>|2-x|(10分)
)?f(2x+1)>f(3-x)?|2x|>|2-x|(10分)解得,
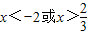 (14分)
(14分)综上:f(
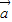 •
•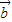 )>f(
)>f(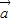 •
•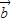 )的解集为
)的解集为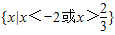 .
.点评:本题考查不等式的解集的求法,转化思想的应用,向量数量积的应用,考查计算能力.

练习册系列答案
相关题目