题目内容
(本小题满分12分)已知函数 ,
, .
.
(Ⅰ) 时,证明:
时,证明: ;
;
(Ⅱ) ,若
,若 ,求a的取值范围.
,求a的取值范围.
(1)证明详见解析;(2)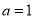 .
.
【解析】
试题分析:本题主要考查导数的运算、利用导数判断函数的单调性、利用导数求函数的最值和极值等基础知识,意在考查考生的分析问题解决问题的能力、转化能力、运算求解能力.第一问,对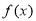 求导,再构造函数
求导,再构造函数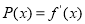 进行二次求导,通过对
进行二次求导,通过对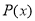 的分析,得到
的分析,得到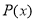 的最小值,从而得到
的最小值,从而得到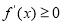 ,判断得出
,判断得出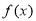 在
在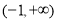 内单调递增,从而求出最小值;第二问,构造
内单调递增,从而求出最小值;第二问,构造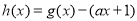 ,对
,对 求导,需构造函数
求导,需构造函数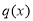 进行二次求导,结合第一问的结论,可得
进行二次求导,结合第一问的结论,可得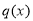 在
在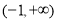 单调递减,然后对
单调递减,然后对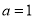 、
、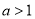 、
、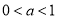 进行讨论,证明
进行讨论,证明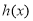 的最大值小于等于0即可.
的最大值小于等于0即可.
试题解析:(Ⅰ)令p(x)=f(x)=ex-x-1,p(x)=ex-1,
在(-1,0)内,p(x)<0,p(x)单减;在(0,+∞)内,p(x) >0,p(x)单增.
所以p(x)的最小值为p(0)=0,即f(x)≥0,
所以f(x)在(-1,+∞)内单调递增,即f(x)>f(-1)>0. 4分
(Ⅱ)令h(x)=g(x)-(ax+1),则h(x)=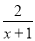 -e-x-a,
-e-x-a,
令q(x)=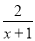 -e-x-a,q(x)=
-e-x-a,q(x)=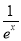 -
-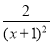 .
.
由(Ⅰ)得q(x)<0,则q(x)在(-1,+∞)上单调递减. 6分
(1)当a=1时,q(0)=h(0)=0且h(0)=0.
在(-1,0)上h(x)>0,h(x)单调递增,在(0,+∞)上h'(x)<0,h(x)单调递减,
所以h(x)的最大值为h(0),即h(x)≤0恒成立. 7分
(2)当a>1时,h(0)<0,
x∈(-1,0)时,h(x)=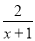 -e-x-a<
-e-x-a<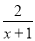 -1-a=0,解得x=
-1-a=0,解得x=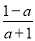 ∈(-1,0).
∈(-1,0).
即x∈(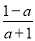 ,0)时h(x)<0,h(x)单调递减,
,0)时h(x)<0,h(x)单调递减,
又h(0)=0,所以此时h(x)>0,与h(x)≤0恒成立矛盾. 9分
(3)当0<a<1时,h(0)>0,
x∈(0,+∞)时,h(x)=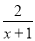 -e-x-a>
-e-x-a>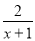 -1-a=0,解得x=
-1-a=0,解得x=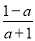 ∈(0,+∞).
∈(0,+∞).
即x∈(0,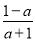 )时h(x)>0,h(x)单调递增,
)时h(x)>0,h(x)单调递增,
又h(0)=0,所以此时h(x)>0,与h(x)≤0恒成立矛盾. 11分
综上,a的取值为1. 12分
考点:导数的运算、利用导数判断函数的单调性、利用导数求函数的最值和极值.
考点分析: 考点1:对数函数 试题属性- 题型:
- 难度:
- 考核:
- 年级:

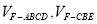 ,求
,求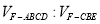 .
. 满足
满足 ,则
,则 B.
B.  C.
C.  D.
D. 
 ,则
,则 ( )
( ) B.
B. C.
C. 或0
或0 ( )
( ) B.
B. C.
C. D.
D.
 ,满足
,满足 ,则
,则 的取值范围为 .
的取值范围为 . 的值域为( )
的值域为( ) B.
B. C.
C. D.
D.
 ,点
,点 为坐标原点, 点
为坐标原点, 点 N
N , 向量
, 向量 ,
, 是向量
是向量 与
与 的夹角,则
的夹角,则 的值为 .
的值为 . 中,
中, ,
, ,
, 是
是 的个位数字,
的个位数字, 是
是 的前
的前 项和,则
项和,则 .
.