题目内容
数列{an}的前n项和为Sn，已知Sn+an=-n（n∈N*）恒成立．
（1）求数列{an}的通项公式；
（2）bn=ln（an+1），求{anbn}的前n项和；
（3）求证：
．
（1）解：∵Sn+an=-n①
∴n≥2时，Sn-1+an-1=-n+1②
①-②可得2an=an-1-1
∴2（an+1）=an-1+1
又a1=-
，∴{an+1}是以为首项，为公比的等比数列
∴an+1=
，∴an=-1；
（2）解：bn=ln（an+1）=nln，∴anbn=[-1]•nln，
∴{anbn}的前n项和为ln[+2•
+…+n•]-
•ln
令Tn=ln[+2•+…+n•]，则Tn=ln[+2•
+…+（n-1）•+n•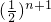
]，
两式相减，可得Tn=ln（2-
-
）
∴{anbn}的前n项和为ln（2--）-•ln；
（3）证明：由（1）知，
=-2（
-
）
∴
=-2（
+
+…+-）
=-2（
）＜2
∴．
分析：（1）再写一式，两式相减，可得{an+1}是以为首项，为公比的等比数列，从而可得数列{an}的通项公式；
（2）确定数列的通项，利用错位相减法求和；
（3）确定通项，利用裂项法求和，即可证得结论．
点评：本题考查数列的通项与求和，考查不等式的证明，正确运用数列的求和方法是关键．
∴n≥2时，Sn-1+an-1=-n+1②
①-②可得2an=an-1-1
∴2（an+1）=an-1+1
又a1=-
，∴{an+1}是以为首项，为公比的等比数列∴an+1=
，∴an=-1；（2）解：bn=ln（an+1）=nln
，∴anbn=[-1]•nln，∴{anbn}的前n项和为ln
[+2•+…+n•]-•ln令Tn=ln
[+2•+…+n•]，则Tn=ln[+2•+…+（n-1）•+n•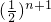]，两式相减，可得Tn=ln
（2--）∴{anbn}的前n项和为ln
（2--）-•ln；（3）证明：由（1）知，
=-2（-）∴
=-2（++…+-）=-2（
）＜2∴
．分析：（1）再写一式，两式相减，可得{an+1}是以
为首项，为公比的等比数列，从而可得数列{an}的通项公式；（2）确定数列的通项，利用错位相减法求和；
（3）确定通项，利用裂项法求和，即可证得结论．
点评：本题考查数列的通项与求和，考查不等式的证明，正确运用数列的求和方法是关键．
练习册系列答案
相关题目