Question

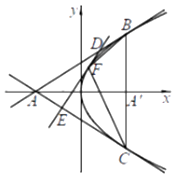
【题目】如图，AB与圆O相切于点B，CD为圆O上两点，延长AD交圆O于点E，BF∥CD且交ED于点F
（Ⅰ）证明：△BCE∽△FDB；
（Ⅱ）若BE为圆O的直径，∠EBF=∠CBD，BF=2，求ADED．

Answer 1

【答案】解：

（Ⅰ）证明：∵BF∥CD；

∴∠EDC=∠BFD，

又∠EBC=∠EDC，

∴∠EBC=∠BFD，

又∠BCE=∠BDF，

∴△BCE∽△FDB．

（Ⅱ）因为∠EBF=∠CBD，所以∠EBC=∠FBD，

由（Ⅰ）得∠EBC=∠BFD，所以∠FBD=∠BFD，

又因为BE为圆O的直径，

所以△FDB为等腰直角三角形，BD= BF= ，

因为AB与圆O相切于B，所以EB⊥AB，即ADED=BD2=2

【解析】（Ⅰ）根据BF∥CD便有∠EDC=∠BFD，再根据同一条弦所对的圆周角相等即可得出∠EBC=∠BFD，∠BCE=∠BDF，这样即可得出：△BCE与△FDB相似；（Ⅱ）根据条件便可得出∠EBC=∠FBD，再由上面即可得出∠FBD=∠BFD，这样即可得出△FDB为等腰直角三角形，从而可求出BD= ，根据射影定理即可求出ADED的值．
【考点精析】掌握相似三角形的判定是解答本题的根本，需要知道相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）．