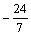题目内容
(本小题满分14分)
已知函数f(x)= sinxcosx-cos2x+
sinxcosx-cos2x+ (x∈R).
(x∈R).
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[0, ]上的值域.
]上的值域.
已知函数f(x)=
 sinxcosx-cos2x+
sinxcosx-cos2x+ (x∈R).
(x∈R).(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[0,
 ]上的值域.
]上的值域.解: (1)f(x)的最小正周期为p. (2)所求的值域为[- ,
,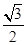 ].
].
 ,
,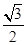 ].
]. 本试题主要是考查了三角函数的化简和函数图像与性质的综合运用。
(1)首先将已知函数利用二倍角公式化简为单一三角函数,结合周期公式求解。
(2)先利用x的范围[0, ],得到2x-
],得到2x-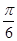 的范围,结合正弦函数图像,求解最值
的范围,结合正弦函数图像,求解最值
解: (1)因为f(x)=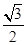 sin2x-
sin2x- cos2x ········· 4分
cos2x ········· 4分
= sin(2x-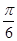 ). ················· 6分
). ················· 6分
故f(x)的最小正周期为p. ············ 8分
(2)当x∈[0, ]时,2x-
]时,2x-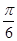 ∈[-
∈[-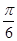 ,
,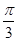 ], ········· 10分
], ········· 10分
故所求的值域为[- ,
,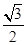 ]. 14分
]. 14分
(1)首先将已知函数利用二倍角公式化简为单一三角函数,结合周期公式求解。
(2)先利用x的范围[0,
 ],得到2x-
],得到2x-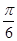 的范围,结合正弦函数图像,求解最值
的范围,结合正弦函数图像,求解最值解: (1)因为f(x)=
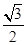 sin2x-
sin2x- cos2x ········· 4分
cos2x ········· 4分= sin(2x-
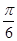 ). ················· 6分
). ················· 6分故f(x)的最小正周期为p. ············ 8分
(2)当x∈[0,
 ]时,2x-
]时,2x-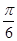 ∈[-
∈[-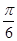 ,
,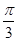 ], ········· 10分
], ········· 10分故所求的值域为[-
 ,
,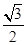 ]. 14分
]. 14分
练习册系列答案
相关题目
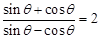 ,求
,求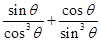 的值
的值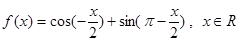
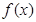 的周期;
的周期;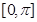 上的减区间;
上的减区间;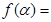
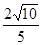 ,
,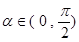 ,求
,求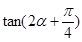 的值
的值 .
.

 ,
, ,那么
,那么 的值是 ( )
的值是 ( )



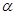 为第三象限角,
为第三象限角,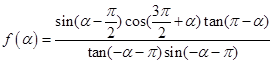 .
.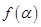
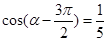 ,求
,求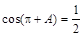 ,则
,则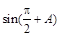 的值是( )
的值是( )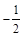
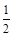
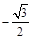
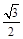
 ,则
,则 的值为_
的值为_  ,
, ,则
,则 ( )
( )