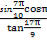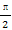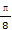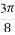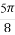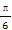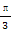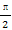题目内容
已知a>0,函数f(x)=-2asin(2x+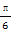
)+2a+b,当x∈[0,
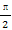]时,-5≤f(x)≤1.
(1)求常数a,b的值.
(2)设g(x)=f(x+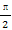)且lg g(x)>0,求g(x)的单调区间.
(1) a=2,b=-5 (2) kπ+
,kπ+
),k∈Z
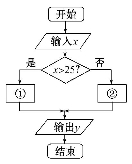
【解析】(1)∵x∈[0,
],
∴2x+∈[,
].
∴sin(2x+)∈[-
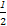,1],
∴-2asin(2x+)∈[-2a,a].
∴f(x)∈[b,3a+b].
又∵-5≤f(x)≤1,∴b=-5,3a+b=1,
因此a=2,b=-5.
(2)由(1)得a=2,b=-5,
∴f(x)=-4sin(2x+)-1,
g(x)=f(x+)=-4sin(2x+)-1
=4sin(2x+)-1,
又由lgg(x)>0得g(x)>1,
∴4sin(2x+)-1>1,
∴sin(2x+)>,
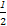∴2kπ+<2x+<2kπ+
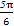,k∈Z,
其中当2kπ+<2x+≤2kπ+,k∈Z时,g(x)单调递增,即kπ<x≤kπ+,k∈Z.
∴g(x)的单调增区间为(kπ,kπ+],k∈Z.
又∵当2kπ+<2x+<2kπ+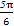,k∈Z时,g(x)单调递减,即kπ+<x<kπ+,k∈Z.
∴g(x)的单调减区间为(kπ+,kπ+),k∈Z.
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
