题目内容
若a,b是任意非零的常数,对于函数y=f(x)有以下5个命题:
①f(x)是T=2a的周期函数的充要条件是f(x+a)=f(x-a);
②f(x)是T=2a的周期函数的充要条件是f(x+a)=-f(x);
③若f(x)是奇函数且是T=2a的周期函数,则f(x)的图形关于直线x=
对称;
④若f(x)关于直线x=
对称,且f(x+a)=-f(x),则f(x)是奇函数;
⑤若f(x)关于点(a,0)对称,关于直线x=b对称,则f(x)是T=4(a-b)的周期函数.
其中正确命题的序号为
①f(x)是T=2a的周期函数的充要条件是f(x+a)=f(x-a);
②f(x)是T=2a的周期函数的充要条件是f(x+a)=-f(x);
③若f(x)是奇函数且是T=2a的周期函数,则f(x)的图形关于直线x=
| a |
| 2 |
④若f(x)关于直线x=
| a |
| 2 |
⑤若f(x)关于点(a,0)对称,关于直线x=b对称,则f(x)是T=4(a-b)的周期函数.
其中正确命题的序号为
①④⑤
①④⑤
.分析:根据函数周期性的定义及充要条件的定义,逐一判断5个命题的真假,综合讨论结果,可得答案.
解答:解:f(x+a)=f(x-a)时,f(x+2a)=f(x),f(x)是T=2a的周期函数
f(x)是T=2a的周期函数时,f(x+a)=f(x-a)一定成立,故①正确;
当f(x+a)=-f(x)时,f(x+2a)=f(x),f(x)是T=2a的周期函数
f(x)是T=2a的周期函数时,f(x+a)=-f(x)不一定成立,
故f(x)是T=2a的周期函数的充分条件是f(x+a)=-f(x),故②错误;
若f(x)是奇函数且是T=2a的周期函数,则f(x)的图形不一定是轴对称图象,故③错误;
若f(x)关于直线x=
对称,则f(a+x)=f(x),又由f(x+a)=-f(x),可得f(x)=-f(-x),即f(x)是奇函数,故④正确;
函数f(x)是以4(m-a)为周期的周期函数.
由条件图象关于点(a,0)对称,故-f(x)=f(2a-x),
又图象关于直线x=b对称,f(2b-x)=f(x),
所以,-f(2b-x)=f(2b-x),即-f(x)=f(2a-2b+x).
由-f(x)=f(2a-2b+x) 得:
-f(2a-2b+x)=f(4a-4b+x),
∴-(-f(x))=f(4a-4b+x),
因此,f[4(a-b)+x]=f(x),
所以,f(x)是以4(a-b)为周期的函数.故⑤正确
故答案为:①④⑤
f(x)是T=2a的周期函数时,f(x+a)=f(x-a)一定成立,故①正确;
当f(x+a)=-f(x)时,f(x+2a)=f(x),f(x)是T=2a的周期函数
f(x)是T=2a的周期函数时,f(x+a)=-f(x)不一定成立,
故f(x)是T=2a的周期函数的充分条件是f(x+a)=-f(x),故②错误;
若f(x)是奇函数且是T=2a的周期函数,则f(x)的图形不一定是轴对称图象,故③错误;
若f(x)关于直线x=
| a |
| 2 |
函数f(x)是以4(m-a)为周期的周期函数.
由条件图象关于点(a,0)对称,故-f(x)=f(2a-x),
又图象关于直线x=b对称,f(2b-x)=f(x),
所以,-f(2b-x)=f(2b-x),即-f(x)=f(2a-2b+x).
由-f(x)=f(2a-2b+x) 得:
-f(2a-2b+x)=f(4a-4b+x),
∴-(-f(x))=f(4a-4b+x),
因此,f[4(a-b)+x]=f(x),
所以,f(x)是以4(a-b)为周期的函数.故⑤正确
故答案为:①④⑤
点评:本题以命题的真假判断为载体,考查了函数的周期性的性质,熟练掌握函数周期性的判定方法是解答的关键.

练习册系列答案
相关题目
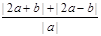 的最小值.
的最小值.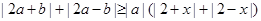 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.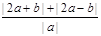 的最小值。
的最小值。 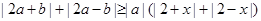 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围. 的最小值.
的最小值.