题目内容
(10分)已知等比数列{ }的前n项和为
}的前n项和为 , 满足
, 满足 (
(
且 均为常数)
均为常数)
(1)求r的值; (4分)
(2)当b=2时,记
 ,求数列
,求数列 的前
的前 项的和
项的和 .(6分)
.(6分)
【答案】
(1)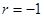 ;(2)证明:见解析。
;(2)证明:见解析。
【解析】本试题主要是考查了等比数列的通项公式和前n项和的求解综合运用。
(1)因为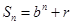 ,
当
,
当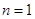 时,
时,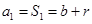 ,
当
,
当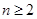 时,
时,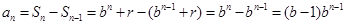 ,得到通项公式。
,得到通项公式。
(2)由(1)得等比数列{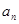 }的首项为
}的首项为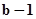 ,公比为
,公比为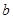 ,
, 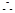
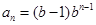 ,利用错位相减法得到结论。
,利用错位相减法得到结论。
解:(1)因为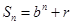 ,
当
,
当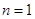 时,
时,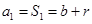 ,
-------1分
,
-------1分
当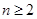 时,
时,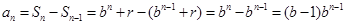 ,
------3分
,
------3分
又因为{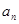 }为等比数列, 所以
}为等比数列, 所以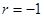 , -------------------4分
, -------------------4分
(2)证明:
由(1)得等比数列{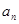 }的首项为
}的首项为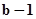 ,公比为
,公比为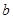 ,
, 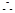
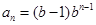 -------5分
-------5分
当b=2时,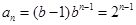 ,
,  ------6分
------6分
设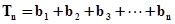 ,则
,则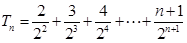
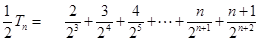 ----------------7分
----------------7分
两式相减, 得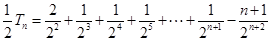 -------8分
-------8分
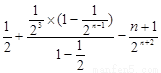
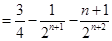 -------------9分
-------------9分
所以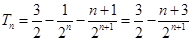 --------10分
--------10分

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知等比数列{an}的前三项依次为t,t-2,t-3.则an=( )
A、4-(
| ||
| B、4-2n | ||
C、4•(
| ||
| D、4-2n-1 |