Question

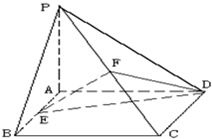如图，在四棱锥P-ABCD中，底面ABCD是矩形，侧棱PA垂直于底面，E、F分别是AB、PC的中点．
（1）求证：CD⊥PD；   
（2）求证：EF∥平面PAD；
（3）若直线EF⊥平面PCD，那么

|PA|

|AD|

=？

Answer 1

分析：（1）证明PA⊥CD，AD⊥CD，证得CD⊥平面PAD，从而有CD⊥PD．
（2）取CD的中点G，由FG是三角形CPD的中位线，可得 FG∥PD，再由举行的性质得 EG∥AD，证明平面EFG∥平面PAD，从而证得EF∥平面PAD．
（3）由条件可得，∠PDA=∠EGF，设PA=x，AD=y，由于tan∠PDA=

PA

AD

=

x

y

，tan∠EGF=

EF

FG

=

3y2-x2

x2+y2

，得到

x

y

=

3y2-x2

x2+y2

，化简得 (

x

y

)4+2 (

x

y

)2-3 = 0，解方程求得

x

y

的值．

解答：解：（1）证明：∵侧棱PA垂直于底面，∴PA⊥CD．又底面ABCD是矩形，∴AD⊥CD，
这样，CD垂直于平面PAD内的两条相交直线，∴CD⊥平面PAD，∴CD⊥PD．
（2）取CD的中点G，∵E、F分别是AB、PC的中点，∴FG是三角形CPD的中位线，
∴FG∥PD，FG∥面PAD．∵底面ABCD是矩形，∴EG∥AD，EG∥平面PAD．
故平面EFG∥平面PAD，∴EF∥平面PAD．
（3）∵直线EF⊥平面PCD，∴EF⊥FG．设PA=x，AD=y，则 PD=

x2+ y2

．
由于∠PDA 和∠EGF的两边分别平行，故∠PDA=∠EGF． EF=

EG2- FG2

=

AD2-( PD 2 )2

=

3y2-x2

2

，
∵tan∠PDA=

PA

AD

=

x

y

，tan∠EGF=

EF

FG

=

3y2-x2 2

x2+y2 2

=

3y2-x2

x2+y2

，
∴

x

y

=

3y2-x2

x2+y2

，∴x⁴+2x²y²-3y⁴=0，∴(

x

y

)4+2 (

x

y

)2-3 = 0，
∴(

x

y

)2=-3（舍去），或  (

x

y

)2=1，∴

x

y

=1，即

PA

AD

=1．

点评：本题考查证明线线垂直、线面平行的方法，以及求线段长度之比，判断∠PDA=∠EGF 是解题的关键．