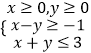题目内容
【题目】在平面直角坐标系![]() 中,
中, ![]() ,
, ![]() 两点的坐标分别为
两点的坐标分别为![]() ,
, ![]() ,动点
,动点![]() 满足:直线
满足:直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
, ![]() 分别交曲线
分别交曲线![]() 于
于![]() ,
, ![]() 两点,设
两点,设![]() 的斜率为
的斜率为![]() (
(![]() ),
),![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析: (1)设动点![]() 的坐标
的坐标![]() ,由
,由![]() ,求出点
,求出点![]() 的轨迹
的轨迹![]() 的方程; (2)设
的方程; (2)设![]() 点坐标为
点坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,与
,与![]() 联立求出
联立求出![]() 的坐标用k来表示,进而由弦长公式求出
的坐标用k来表示,进而由弦长公式求出![]() ,
,![]() ,代入面积公式
,代入面积公式![]() ,进而求得
,进而求得![]() ,对关于k的函数求导求出最值即可.
,对关于k的函数求导求出最值即可.
试题解析:解: (Ⅰ)已知![]() ,设动点
,设动点![]() 的坐标
的坐标![]() ,
,
所以直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() (
(![]() ),
),
又![]() ,所以
,所以![]() ,
,
即![]() .
.
(Ⅱ)设![]() 点坐标为
点坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,
,
可得, ![]() ,
,
![]() ,所以
,所以![]()
所以 ,
,
同理![]() ,
,
所以![]() ,
,
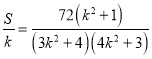 ,
,
令![]()
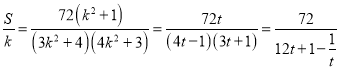 ,
,
令![]() ,
, ![]()
![]() ,
, ![]() 单调递增,
单调递增, ![]()
所以![]() .
.

练习册系列答案
相关题目