题目内容
已知函数y=f(x)=
|
分析:因函数y=
,(-1≤x<0)表示圆x2+y2=1在第二象限的一部分,而函数y=-x+1(0≤x≤1)表示第一象限内的一条线段,通过旋转,组成半球与圆锥体的结合体,所以本题要利用球的表面积公式S=4πr2和圆锥的侧面积公式S=πrl.
| 1-x2 |
解答: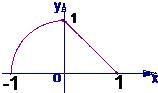 解:y=f(x)=
解:y=f(x)=
的图象如图所示
y=f(x)的曲线绕x轴旋转一周所得几何体是
由一个半径为1的半球及底面半径和高均为1的圆锥体组成,
从而其表面积为(2+
)π.
 解:y=f(x)=
解:y=f(x)=
|
y=f(x)的曲线绕x轴旋转一周所得几何体是
由一个半径为1的半球及底面半径和高均为1的圆锥体组成,
从而其表面积为(2+
| 2 |
点评:本题考查的知识点是旋转体的几何特征,将函数图象与立体几何结合在一起,是一个不错的题型,如2007年上海市高考第21题是:已知半椭圆
+
=1(x≥0)与半椭圆
+
=1(x≤0)组成的曲线称为“果圆”.
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足