Question

7．已知从圆C：x²+y²+2x-4y+3=0外一点P（x₁，y₁）向该圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，则当|PM|取得最小值时点P的坐标为（-$\frac{3}{10}$，$\frac{3}{5}$）．

Answer 1

分析 ⊙C：x²+y²+2x-4y+3=0，化为标准方程，求出圆心C，半径r．设P（x，y）．由切线的性质可得：CM⊥PM，利用|PM|=|PO|，可得2x₁-4y₁+3=0．要使|PM|最小，只要|PO|最小即可．

解答 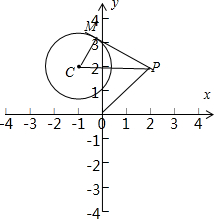解：如图所示，⊙C：x²+y²+2x-4y+3=0化为（x+1）²+（y-2）²=2，圆心C（-1，2），半径r=$\sqrt{2}$．
因为|PM|=|PO|，
所以|PO|²+r²=|PC|²（C为圆心，r为圆的半径），
所以x₁²+y₁²+2=（x₁+1）²+（y₁-2）²，即2x₁-4y₁+3=0．要使|PM|最小，只要|PO|最小即可．
当直线PO垂直于直线2x-4y+3=0时，即直线PO的方程为2x+y=0时，|PM|最小，此时P点即为两直线的交点，得P点坐标（-$\frac{3}{10}$，$\frac{3}{5}$）．
故答案为：（-$\frac{3}{10}$，$\frac{3}{5}$）．

点评 本题考查了圆的切线的性质、勾股定理、两点之间的距离公式，考查了推理能力与计算能力，属于中档题．