题目内容
15.直线(a-1)x-y+2a+1=0恒过定点(-2,3).分析 把直线的方程分离参数,令参数的系数等于0,求得x、y的值,可得此直线经过的定点的坐标.
解答 解:直线(a-1)x-y+2a+1=0,即 a(x+2)+(-x-y+1)=0,
令x+2=0,求得y=3,可得此直线经过定点(-2,3),
故答案为:(-2,3).
点评 本题主要考查直线过定点问题,利用了m(ax+by+c)+(a′x+b′y+c′)=0 经过直线ax+by+c=0和直线a′x+b′y+c′=0的交点,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
6.F1,F2分别为椭圆$\frac{x^2}{4}+\frac{y^2}{2}$=1的左右焦点,P为椭圆上一动点,F2关于直线PF1的对称点为M,F1关于直线PF2的对称点为N,则当|MN|的最大值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | $2\sqrt{2}$ |
10.已知定义在R上的奇函数f(x)满足f(x)=2x-4(x>0),则{x|f(x-1)>0}等于( )
| A. | {x|x>3} | B. | {x|-1<x<1} | C. | {x|-1<x<1或x>3} | D. | {x|x<-1} |
4.“m>0”是“方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{m}$=1表示椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
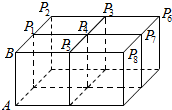 如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )
如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )