题目内容
(本小题共14分)
已知椭圆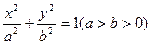 的离心率为
的离心率为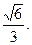
(I)若原点到直线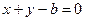 的距离为
的距离为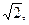 求椭圆的方程;
求椭圆的方程;
(II)设过椭圆的右焦点且倾斜角为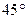 的直线
的直线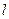 和椭圆交于A,B两点.
和椭圆交于A,B两点.
(i)当 ,求b的值;
,求b的值;
(ii)对于椭圆上任一点M,若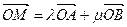 ,求实数
,求实数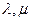 满足的关系式.
满足的关系式.
已知椭圆
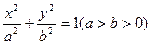 的离心率为
的离心率为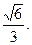
(I)若原点到直线
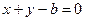 的距离为
的距离为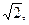 求椭圆的方程;
求椭圆的方程;(II)设过椭圆的右焦点且倾斜角为
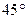 的直线
的直线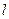 和椭圆交于A,B两点.
和椭圆交于A,B两点.(i)当
 ,求b的值;
,求b的值;(ii)对于椭圆上任一点M,若
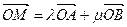 ,求实数
,求实数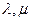 满足的关系式.
满足的关系式.(I)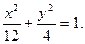
(II)(i)1
(ii)
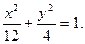
(II)(i)1
(ii)

(I)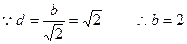
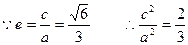
 解得
解得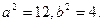
椭圆的方程为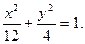 …………………………………………4分
…………………………………………4分
(II)(i) 椭圆的方程可化为:
椭圆的方程可化为:
 ①
①
易知右焦点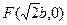 ,据题意有AB:
,据题意有AB: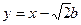 ②
②
由①,②有: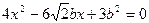 ③
③
设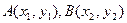 ,
,
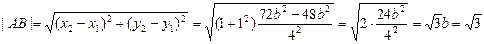
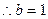 …………………………………………………………8分
…………………………………………………………8分
(ii)显然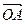 与
与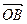 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量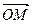 ,有且只有一对实数λ,μ,使得等
,有且只有一对实数λ,μ,使得等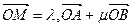 成立.
成立.
设M(x,y),
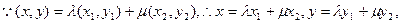
又点M在椭圆上,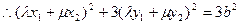 ④
④
由③有: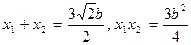
则
 ⑤
⑤
又A,B在椭圆上,故有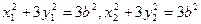 ⑥
⑥
将⑥,⑤代入④可得: ………………………………14分
………………………………14分
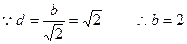
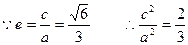
 解得
解得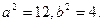
椭圆的方程为
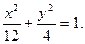 …………………………………………4分
…………………………………………4分(II)(i)
 椭圆的方程可化为:
椭圆的方程可化为: ①
①易知右焦点
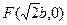 ,据题意有AB:
,据题意有AB: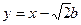 ②
②由①,②有:
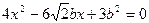 ③
③设
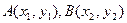 ,
,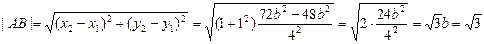
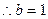 …………………………………………………………8分
…………………………………………………………8分(ii)显然
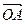 与
与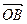 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量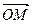 ,有且只有一对实数λ,μ,使得等
,有且只有一对实数λ,μ,使得等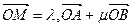 成立.
成立.设M(x,y),
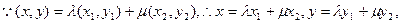
又点M在椭圆上,
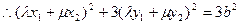 ④
④由③有:
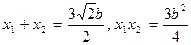
则

 ⑤
⑤又A,B在椭圆上,故有
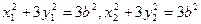 ⑥
⑥将⑥,⑤代入④可得:
 ………………………………14分
………………………………14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
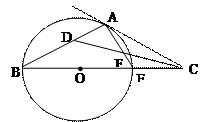
 是
是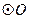 的直径,
的直径,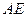 平分
平分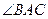 交
交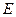 ,过点
,过点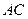 于点
于点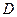 ,试判断
,试判断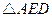 的形状,并说明理由.
的形状,并说明理由.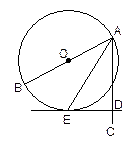
 ,
, ,
, ,
, ,则四边形
,则四边形 的面积为( )
的面积为( )




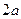 的线段
的线段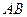 的两个端点
的两个端点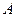 和
和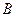 分别在
分别在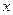 轴和
轴和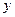 轴上滑动,求线段
轴上滑动,求线段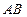 是圆
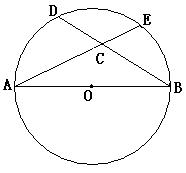
是圆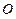 的直径,
的直径,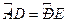 ,
,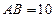 ,
,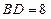 ,则
,则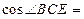 .
.
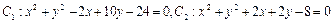 ,则以两圆公共弦为直径的圆的方程是 .
,则以两圆公共弦为直径的圆的方程是 .  是圆
是圆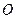 上的点,且
上的点,且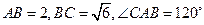 ,则
,则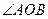 对应的劣弧长为 .
对应的劣弧长为 .