题目内容
若任意满足
|
分析:此题考查的是线性规划以及恒成立问题.在分析时,可以先有线性约束条件画出可行域,然后由恒成立的条件可转化为求
的目标函数求最值即可,进而利用可行域即可获得答案.
| y |
| x |
解答: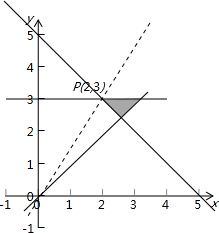 解:由题意知:可行域如图,
解:由题意知:可行域如图,
又∵a(x2+y2)≤(x+y)2在可行域内恒成立.
且a≤
=1+
=1+
=1+
,
故只求Z=
+
的最大值即可.
由图象可知:1≤
≤
,即1≤
≤
,
∴当
=
时Z取到最大值,最大值为
,
故a≤1+
=
,
所以答案为
.
 解:由题意知:可行域如图,
解:由题意知:可行域如图,又∵a(x2+y2)≤(x+y)2在可行域内恒成立.
且a≤
| (x+y)2 |
| x2+y2 |
| 2xy |
| x2+y2 |
2
| ||
1+(
|
| 2 | ||||||
|
故只求Z=
| y |
| x |
| 1 | ||
|
由图象可知:1≤
| y |
| x |
| 3-0 |
| 2-0 |
| y |
| x |
| 3 |
| 2 |
∴当
| y |
| x |
| 3 |
| 2 |
| 13 |
| 6 |
故a≤1+
| 2 | ||
|
| 25 |
| 13 |
所以答案为
| 25 |
| 13 |
点评:本题属于对线性规划、基本不等式、还有函数知识考查的综合类题目.在解答过程当中,同学们应该仔细体会数形结合的思想、函数思想、转化思想还有恒成立思想在题目中的体现.故本题值得思考总结.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目