题目内容
设函数y=f(x)是定义在R+上的减函数,并且满足f(xy)=f(x)+f(y),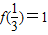 .
.(1)求f(1)的值;
(2)如果f(x)+f(2-x)<2,求x的取值范围.
【答案】分析:(1)利用赋值法:令x=y=1即可求解
(2)利用赋值法可得,f( )=2,然后结合f(xy)=f(x)+f(y),转化已知不等式,从而可求
)=2,然后结合f(xy)=f(x)+f(y),转化已知不等式,从而可求
解答:解:(1)令x=y=1,则f(1)=f(1)+f(1),
∴f(1)=0(4分)
(2)∵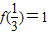
∴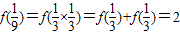
∴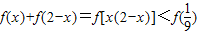 ,
,
又由y=f(x)是定义在R+上的减函数,得: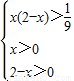
解之得: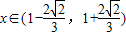 . …(12分)
. …(12分)
点评:本题主要考查了利用赋值法求解抽象函数的函数值,及利用函数的单调性求解不等式,属于函数知识的综合应用
(2)利用赋值法可得,f(
 )=2,然后结合f(xy)=f(x)+f(y),转化已知不等式,从而可求
)=2,然后结合f(xy)=f(x)+f(y),转化已知不等式,从而可求解答:解:(1)令x=y=1,则f(1)=f(1)+f(1),
∴f(1)=0(4分)
(2)∵
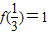
∴
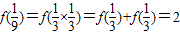
∴
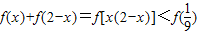 ,
,又由y=f(x)是定义在R+上的减函数,得:
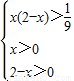
解之得:
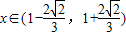 . …(12分)
. …(12分)点评:本题主要考查了利用赋值法求解抽象函数的函数值,及利用函数的单调性求解不等式,属于函数知识的综合应用

练习册系列答案
相关题目