题目内容
已知函数f(x)是定义在R上的奇函数,f(1)=0,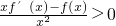 (x>0),则不等式
(x>0),则不等式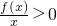 的解集是________.
的解集是________.
(-∞,-1)∪(1,+∞)
分析:先由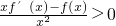 ,得函数g(x)=
,得函数g(x)= 在(0,+∞)上为增函数,再由函数f(x)是定义在R上的奇函数,函数g(x)=
在(0,+∞)上为增函数,再由函数f(x)是定义在R上的奇函数,函数g(x)= 在R上为偶函数,从而画出函数的示意图,数形结合解不等式即可
在R上为偶函数,从而画出函数的示意图,数形结合解不等式即可
解答:依题意,f(1)=0
由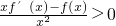 ,得函数g(x)=
,得函数g(x)= 在(0,+∞)上为增函数
在(0,+∞)上为增函数
又由g(-x)= =
= =g(x),得函数g(x)=
=g(x),得函数g(x)= 在R上为偶函数
在R上为偶函数
∴函数g(x)= 在(-∞,0)上为减函数
在(-∞,0)上为减函数
且g(1)=0,g(-1)=0
由图可知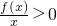 的解集是(-∞,-1)∪(1,+∞)
的解集是(-∞,-1)∪(1,+∞)
故答案为(-∞,-1)∪(1,+∞)
点评:本题综合考察了导数的四则运算,导数在函数单调性中的应用,及函数奇偶性的判断和性质,解题时要能根据性质画示意图,数形结合解决问题
分析:先由
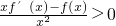 ,得函数g(x)=
,得函数g(x)= 在(0,+∞)上为增函数,再由函数f(x)是定义在R上的奇函数,函数g(x)=
在(0,+∞)上为增函数,再由函数f(x)是定义在R上的奇函数,函数g(x)= 在R上为偶函数,从而画出函数的示意图,数形结合解不等式即可
在R上为偶函数,从而画出函数的示意图,数形结合解不等式即可解答:依题意,f(1)=0
由
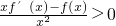 ,得函数g(x)=
,得函数g(x)= 在(0,+∞)上为增函数
在(0,+∞)上为增函数
又由g(-x)=
 =
= =g(x),得函数g(x)=
=g(x),得函数g(x)= 在R上为偶函数
在R上为偶函数∴函数g(x)=
 在(-∞,0)上为减函数
在(-∞,0)上为减函数且g(1)=0,g(-1)=0
由图可知
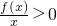 的解集是(-∞,-1)∪(1,+∞)
的解集是(-∞,-1)∪(1,+∞)故答案为(-∞,-1)∪(1,+∞)
点评:本题综合考察了导数的四则运算,导数在函数单调性中的应用,及函数奇偶性的判断和性质,解题时要能根据性质画示意图,数形结合解决问题

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+