题目内容
P是△ABC所在平面上一点,若 ,则P是△ABC 的( )
,则P是△ABC 的( )
| A.重心 | B.内心 | C.垂心 | D.外心 |
C
解析试题分析:根据题意,由于 ,所以
,所以 ,同理可知
,同理可知 ,因此可知,点P是三角形ABC的垂心,故选C.
,因此可知,点P是三角形ABC的垂心,故选C.
考点:三角形的垂心
点评:解决的关键是利用向量的加减法变形得到向量的数量积为零证明垂直,属于基础题。

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
在四面体 中,点
中,点 为棱
为棱 的中点. 设
的中点. 设 ,
,  ,
, ,那么向量
,那么向量 用基底
用基底 可表示为( )
可表示为( )
A. | B. |
C. | D. |
已知A(a,0),B(0,a)(a>0), =t
=t ,O为坐标原点,则|
,O为坐标原点,则| |的最小值为( )
|的最小值为( )
A. a a | B. a a | C. a a | D.a |
空间四边形 中,
中,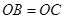 ,
, ,则
,则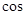 <
<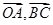 >的值是( )
>的值是( )
A. | B. | C.- | D. |
已知 与
与 为互相垂直的单位向量,
为互相垂直的单位向量,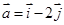 ,
, 且
且 与
与 的夹角为锐角,则实数
的夹角为锐角,则实数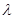 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
若向量 和向量
和向量 平行,则
平行,则  ( )
( )
A. | B. | C. | D. |
平面向量 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则

A. | B. | C.4 | D.12 |
、若 ,且
,且 ,则实数
,则实数 的值是( )
的值是( )
| A.-1 | B.0  | C.1 | D.-2 |
 =
=
 ,
, =
=
 ,
, =λ
=λ ,则λ的值为( )
,则λ的值为( )

