题目内容
已知f(x)=(1+x)α(1+ )β(α,β,x∈R+),
)β(α,β,x∈R+),
(1)求f(x)的最小值;
(2)如果y>0,求证:(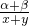 )α+β≤(
)α+β≤(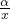 )α•(
)α•(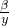 )β;
)β;
(3)如果α1,α2,…αn,β1,β2,…βn>0,求证:(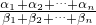 )α1+α2+…+αn≤(
)α1+α2+…+αn≤(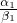 )α1•(
)α1•(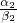 )α2…(
)α2…(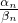 )αn.
)αn.
(1)解:f′(x)=α(1+x)α-1(1+ )β+(1+x)α•β(1+
)β+(1+x)α•β(1+ )β-1•(-1)•
)β-1•(-1)• =
= ,
,
∵x∈( ,∞)时f′(x)>0,x∈(0,
,∞)时f′(x)>0,x∈(0, )时,f′(x)<0.
)时,f′(x)<0.
∴f(x)max=f( )=(
)=(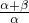 )α(
)α(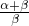 )β.
)β.
(2)证:∵f( )≤f(
)≤f( ),∴(
),∴(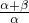 )α•(
)α•(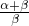 )β≤(
)β≤( )α•(
)α•(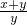 )β,
)β,
即(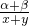 )α+β≤(
)α+β≤(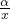 )α•(
)α•(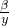 )β.
)β.
(3)当n=2时,由(2)可知(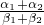 )α1+α2≤(
)α1+α2≤(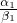 )α1•(
)α1•(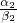 )α2,
)α2,
设n=k时,(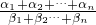 )α1+α2+…+αn≤(
)α1+α2+…+αn≤(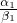 )α1•(
)α1•(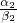 )α2…(
)α2…(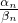 )αn,
)αn,
当n=k+1时,(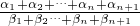 )α1+α2+…+αn+αn+1
)α1+α2+…+αn+αn+1
=[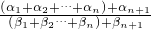 ](α1+α2+…+αn)+αn+1
](α1+α2+…+αn)+αn+1
≤(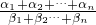 )α1+α2+…+αn•(
)α1+α2+…+αn•(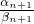 )αn+1
)αn+1
≤(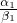 )α1•(
)α1•(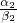 )α2…(
)α2…(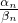 )αn•(
)αn•(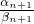 )αn+1.
)αn+1.
所以,结论对一切n成立.
分析:(1)先求导函数得f′(x)= ,从而可知x∈(
,从而可知x∈( ,+∞)时f′(x)>0,x∈(0,
,+∞)时f′(x)>0,x∈(0, )时,f′(x)<0.故可求f(x)的最小值;
)时,f′(x)<0.故可求f(x)的最小值;
(2)根据f( )≤f(
)≤f( ),可得(
),可得(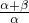 )α•(
)α•(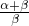 )β≤(
)β≤( )α•(
)α•(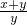 )β,从而得证;
)β,从而得证;
(3)利用数学归纳法证明,当n=2时,由(2)可知(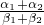 )α1+α2≤(
)α1+α2≤(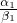 )α1•(
)α1•(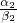 )α2,假设n=k时,成立,即(
)α2,假设n=k时,成立,即(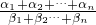 )α1+α2+…+αn≤(
)α1+α2+…+αn≤(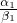 )α1•(
)α1•(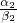 )α2…(
)α2…(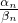 )αn,再证明当n=k+1时也,成立.
)αn,再证明当n=k+1时也,成立.
点评:本题以函数为载体,考查导数的运用,考查函数与不等式的综合,考查数学归纳法,有一定的综合性.
 )β+(1+x)α•β(1+
)β+(1+x)α•β(1+ )β-1•(-1)•
)β-1•(-1)• =
= ,
,∵x∈(
 ,∞)时f′(x)>0,x∈(0,
,∞)时f′(x)>0,x∈(0, )时,f′(x)<0.
)时,f′(x)<0.∴f(x)max=f(
 )=(
)=(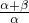 )α(
)α(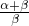 )β.
)β.(2)证:∵f(
 )≤f(
)≤f( ),∴(
),∴(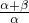 )α•(
)α•(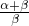 )β≤(
)β≤( )α•(
)α•(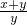 )β,
)β,即(
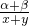 )α+β≤(
)α+β≤(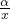 )α•(
)α•(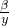 )β.
)β.(3)当n=2时,由(2)可知(
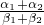 )α1+α2≤(
)α1+α2≤(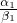 )α1•(
)α1•(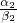 )α2,
)α2,设n=k时,(
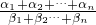 )α1+α2+…+αn≤(
)α1+α2+…+αn≤(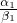 )α1•(
)α1•(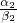 )α2…(
)α2…(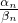 )αn,
)αn,当n=k+1时,(
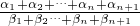 )α1+α2+…+αn+αn+1
)α1+α2+…+αn+αn+1=[
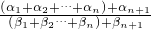 ](α1+α2+…+αn)+αn+1
](α1+α2+…+αn)+αn+1≤(
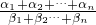 )α1+α2+…+αn•(
)α1+α2+…+αn•(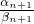 )αn+1
)αn+1≤(
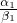 )α1•(
)α1•(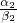 )α2…(
)α2…(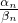 )αn•(
)αn•(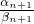 )αn+1.
)αn+1.所以,结论对一切n成立.
分析:(1)先求导函数得f′(x)=
 ,从而可知x∈(
,从而可知x∈( ,+∞)时f′(x)>0,x∈(0,
,+∞)时f′(x)>0,x∈(0, )时,f′(x)<0.故可求f(x)的最小值;
)时,f′(x)<0.故可求f(x)的最小值;(2)根据f(
 )≤f(
)≤f( ),可得(
),可得(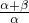 )α•(
)α•(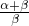 )β≤(
)β≤( )α•(
)α•(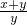 )β,从而得证;
)β,从而得证;(3)利用数学归纳法证明,当n=2时,由(2)可知(
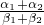 )α1+α2≤(
)α1+α2≤(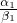 )α1•(
)α1•(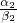 )α2,假设n=k时,成立,即(
)α2,假设n=k时,成立,即(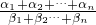 )α1+α2+…+αn≤(
)α1+α2+…+αn≤(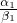 )α1•(
)α1•(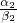 )α2…(
)α2…(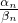 )αn,再证明当n=k+1时也,成立.
)αn,再证明当n=k+1时也,成立.点评:本题以函数为载体,考查导数的运用,考查函数与不等式的综合,考查数学归纳法,有一定的综合性.

练习册系列答案
相关题目
已知f(x)=a-
是定义在R上的奇函数,则f-1(-
)的值是( )
| 2 |
| 2x+1 |
| 3 |
| 5 |
A、
| ||
| B、-2 | ||
C、
| ||
D、
|