Question

（2013•许昌三模）如图，多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AB=CD=1，AC=

3

，AD=DE=2，G为AD的中点．
（1）求证；AC⊥CE；
（2）在线段CE上找一点F，使得BF∥平面ACD，并给予证明；
（3）求三棱锥V_G-BCE的体积．

Answer 1

分析：（1）利用线面垂直的性质定理即可得出DE⊥AC；根据勾股定理的逆定理可得AC⊥CD，利用线面垂直的判定定理可得AC⊥平面CDE，
（2）利用线面垂直的性质定理可得AB∥ED，设F为线段CE的中点，H是线段CD的中点，利用三角形的中位线定理可得FH

∥

.

1

2

ED，又AB

∥

.

1

2

ED，于是可得四边形ABFH为平行四边形，可得BF∥AH，再利用线面平行的判定定理即可证明；
（3）作CP⊥AD垂足为P，利用面面垂直的性质定理可得CP⊥平面ABED，再利用VG-BCE=VC-BGE=

1

3

S△BGE•CP，即可得出体积．

解答：（1）证明：∵DE⊥平面ACD，∴DE⊥AC，
AC=

3

，CD=1，AD=2，∴AD²=AC²+CD²，∴AC⊥CD．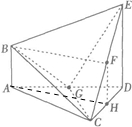
∴CD∩DE=D，∴AC⊥平面CDE．
∴AC⊥CE．
（2）由已知AB⊥平面ACD，DE⊥平面ACD，∴AB∥ED，
设F为线段CE的中点，H是线段CD的中点，
连接FH，则FH

∥ .

.

1

2

ED，∴FH

∥ .

.

AB，
∴四边形ABFH是平行四边形，∴BF∥AH，
由BF?平面ACD内，AH?平面ACD，∴BF∥平面ACD；
（3）由ED⊥平面ACD，∴平面ABED⊥平面ACD，
在平面ACD内作CP⊥AD垂足为P，
∵平面ABED∩平面ACD=AD，∴CP⊥平面ABED，CP为三棱锥V_C-BGE的高．
由VG-BCE=VC-BGE=

1

3

S△BGE•CP，
∵S梯形ABED=

AD(AB+ED)

2

=

2×(1+2)

2

=3，S△ABG=

1

2

×1×1=

1

2

，S△DGE=

1

2

×1×2=1．
∴S△BGE=S梯形ABED-S△ABG-S△DGE=3-

1

2

-1=

3

2

，
∵

1

2

AC•CD=

1

2

AD•CP，CP=

3

2

．
∴三棱锥V_G-BCE的体积VG-BCE=VC-BGE=

1

3

S△BGE•CP=

1

3

×

3

2

×

3

2

=

3

4

．

点评：熟练掌握线面垂直的判定和性质定理、勾股定理的逆定理、三角形的中位线定理、平行四边形的判定和性质定理、线面平行的判定定理、面面垂直的性质定理、三棱锥的体积计算公式和“等积变形”是解题的关键．