题目内容
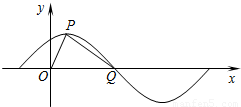
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<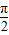 )图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|OQ|=2,|OP|=
)图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|OQ|=2,|OP|=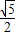 ,|PQ|=
,|PQ|=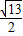 .
.(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)图象向右平移1个单位后得到函数y=g(x)的图象,当x∈[0,2]时,求函数h(x)=f(x)•g(x)的最大值.
【答案】分析:(Ⅰ)由余弦定理得cos∠POQ 的值,可得sin∠POQ,求出P的坐标可得A的值,再由函数的周期求出ω的值,再把点P的坐标代入函数解析式求出φ,即可求得 y=f(x) 的解析式.
(Ⅱ)求出g(x) 的解析式,化简h(x)=f(x)g(x) 的解析式为 sin(
sin(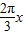 -
-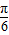 )+
)+ ,再根据x的范围求出h(x) 的值域,从而求得h(x) 的最大值.
,再根据x的范围求出h(x) 的值域,从而求得h(x) 的最大值.
解答:解:(Ⅰ)由余弦定理得cos∠POQ=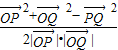 =
=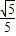 ,…(2分)
,…(2分)
∴sin∠POQ=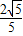 ,得P点坐标为(
,得P点坐标为( ,1),∴A=1,
,1),∴A=1,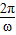 =4(2-
=4(2- ),∴ω=
),∴ω=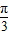 . …(5分)
. …(5分)
由f( )=sin(
)=sin(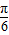 +φ)=1 可得 φ=
+φ)=1 可得 φ=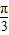 ,∴y=f(x) 的解析式为 f(x)=sin(
,∴y=f(x) 的解析式为 f(x)=sin(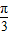 x+
x+ ).…(6分)
).…(6分)
(Ⅱ)根据函数y=Asin(ωx+∅)的图象变换规律求得 g(x)=sin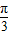 x,…(7分)
x,…(7分)
h(x)=f(x)g(x)=sin(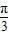 x+
x+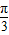 ) sin
) sin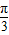 x=
x=
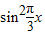 +
+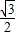 sin
sin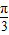 xcos
xcos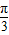 x
x
=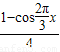 +
+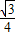 sin
sin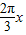 =
= sin(
sin(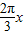 -
-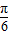 )+
)+ .…(10分)
.…(10分)
当x∈[0,2]时,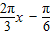 ∈[-
∈[-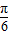 ,
,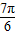 ],
],
∴当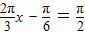 ,
,
即 x=1时,hmax(x)= .…(12分)
.…(12分)
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,函数y=Asin(ωx+∅)的图象变换规律,正弦函数的定义域和值域,属于中档题.
(Ⅱ)求出g(x) 的解析式,化简h(x)=f(x)g(x) 的解析式为
 sin(
sin(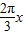 -
-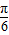 )+
)+ ,再根据x的范围求出h(x) 的值域,从而求得h(x) 的最大值.
,再根据x的范围求出h(x) 的值域,从而求得h(x) 的最大值.解答:解:(Ⅰ)由余弦定理得cos∠POQ=
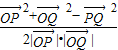 =
=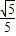 ,…(2分)
,…(2分)∴sin∠POQ=
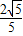 ,得P点坐标为(
,得P点坐标为( ,1),∴A=1,
,1),∴A=1,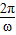 =4(2-
=4(2- ),∴ω=
),∴ω=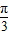 . …(5分)
. …(5分)由f(
 )=sin(
)=sin(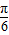 +φ)=1 可得 φ=
+φ)=1 可得 φ=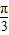 ,∴y=f(x) 的解析式为 f(x)=sin(
,∴y=f(x) 的解析式为 f(x)=sin(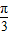 x+
x+ ).…(6分)
).…(6分)(Ⅱ)根据函数y=Asin(ωx+∅)的图象变换规律求得 g(x)=sin
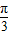 x,…(7分)
x,…(7分)h(x)=f(x)g(x)=sin(
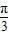 x+
x+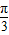 ) sin
) sin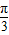 x=
x=
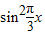 +
+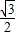 sin
sin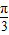 xcos
xcos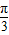 x
x =
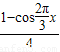 +
+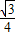 sin
sin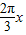 =
= sin(
sin(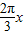 -
-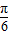 )+
)+ .…(10分)
.…(10分)当x∈[0,2]时,
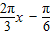 ∈[-
∈[-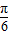 ,
,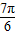 ],
],∴当
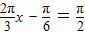 ,
,即 x=1时,hmax(x)=
 .…(12分)
.…(12分)点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,函数y=Asin(ωx+∅)的图象变换规律,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目