题目内容
已知直线过点P(-2,3),且与两坐标轴围成的三角形面积为4,求直线的方程.
解法一:显然,直线l与两坐标轴不垂直,设直线的方程为y-3=k(x+2).
令x=0,得y=2k+3;令y=0,得x=-![]() -2.
-2.
于是直线与两坐标轴围成的三角形面积为![]() |2k+3|·|
|2k+3|·|![]() +2|=4,即(2k+3)(
+2|=4,即(2k+3)(![]() +2)=±8.
+2)=±8.
若(2k+3)(![]() +2)=8,则整理得4k2+4k+9=0,无解;
+2)=8,则整理得4k2+4k+9=0,无解;
若(2k+3)(![]() +2)=-8,则整理得4k2+20k+9=0,解之,得k=-
+2)=-8,则整理得4k2+20k+9=0,解之,得k=-![]() ,k=-
,k=-![]() .
.
∴所求直线的方程为y-3=-![]() (x+2)或y-3=-
(x+2)或y-3=-![]() (x+2),
(x+2),
即x+2y-4=0和9x+2y+12=0.
解法二:显然,直线在两坐标轴上的截距均不为零.
设所求直线的方程为![]() =1.
=1.
∵点P(-2,3)在直线上,
∴![]() =1. ①
=1. ①
又∵直线与坐标轴围成的面积为4,
∴![]() |a|·|b|=4,即|a|·|b|=8. ②
|a|·|b|=4,即|a|·|b|=8. ②
由①②可得
(1)![]() 或(2)
或(2)![]()
解(1)得![]() 或
或 方程组(2)无解.
方程组(2)无解.
∴所求直线的方程为![]() =1或
=1或
 =1,即x+2y-4=0或9x+2y+12=0.
=1,即x+2y-4=0或9x+2y+12=0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知直线 过点P(2,1),且与
过点P(2,1),且与 ,
, 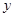 轴所围成的面积为4,则直线
轴所围成的面积为4,则直线 有( )条
有( )条
| A.1 | B.2 | C.3 | D.4 |
 过点P(2,1),且与
过点P(2,1),且与 ,
,  轴所围成的面积为4,则直线
轴所围成的面积为4,则直线