Question

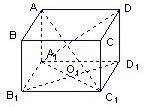如图，在直四棱柱ABCD-A₁B₁C₁D₁中，底面是边长为1的菱形，侧棱长为2．
（1）B₁D₁与A₁D能否垂直？请证明你的判断；
（2）当∠A₁B₁C₁在[

π

3

，

π

2

]上变化时，求异面直线AC₁与A₁B₁所成角的取值范围．

Answer 1

分析：AC∩BD=O，分别以O₁B₁，O₁C₁，O₁O所在直线为x，y，z轴，建立空间直角坐标系，（1）求出

DB1

，

A1D

，计算

D1B

•

A1D

=-2a2≠0说明不垂直；
（2）当∠A₁B₁C₁在[

π

3

，

π

2

]上变化时，求求出

AC1

，

A1B1

，

AC1

•

A1B1

，然后求cos＜

AC1

，

A1B1

＞=

b2

1+b2

，即可求异面直线AC₁与A₁B₁所成角的取值范围．

解答：解：∵菱形A₁B₁C₁D₁中，A₁C₁⊥B₁D₁于O₁，
设AC∩BD=O，分别以O₁B₁，O₁C₁，O₁O所在直线为x，y，z轴，
建立空间直角坐标系，设B₁（a，0，0），C₁（0，b，0）（a²+b²=1），
则D₁（-a，0，0），A₁（0，-b，0），D（-a，0，2）
（1）∵

DB1

=(2a，0，0)，

A1D

=(-a，b，2)，
∴

D1B

•

A1D

=-2a2≠0
∴B₁D₁与A₁D不能垂直．
（2）∵∠A₁B₁C₁∈[

π

3

，

π

2

]，∴

3

3

≤

b

a

≤1，
∵A（0，-b，2）∴

AC1

=(0，2b，-2)，

A1B1

=(a，b，0)，∴

AC1

•

A1B1

=2b2，

|AC1

|=2

b2+1

，

|A1B1

|=

a2+b2

=1，
∴cos＜

AC1

，

A1B1

＞=

b2

1+b2

∵a²+b²=1，∴设a=cosα，b=sinα，又

3

3

≤

b

a

≤1，
∴

3

3

≤tanα≤1，∴

π

6

≤α≤

π

4

∴cos＜

AC1

，

A1B1

＞=

b2

1+b2

=

sin2α

1+sin2α

=

1

1 sin4α + 1 sin2α

=

1

csc4α+csc2α

∵2≤csc²α≤4，∴cos＜

AC1

，

A1B1

＞∈[

5

10

，

6

6

]
∴直线AC₁与A₁B₁所成角的取值范围是[

5

10

，

6

6

]．

点评：本题考查用向量证明垂直，异面直线及其所成的角，考查学生计算能力，是中档题．