题目内容
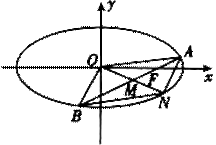
（本小题满分12分）如图，已知椭圆C：
，经过椭圆C的右焦点F且斜率为k（k≠0）的直线l交椭圆C于A、B两点，M为线段AB的中点，设O为椭圆的中心，射线OM交椭圆于N点．（1）是否存在k，使对任意m>0，总有
成立？若存在，求出所有k的值；
（2）若
，求实数k的取值范围．
(Ⅰ) k＝±1 (Ⅱ) 
且k≠0．
解析:
（1）椭圆C：
直线AB：y＝k（x－m）,
，（10k2＋6）x2－20k2mx＋10k2m2－15m2＝0．
设A（x1, y1）、B（x2,y2）,则x1＋x2＝
，x1x2＝
则xm＝
若存在k,使
为ON的中点，∴
．
∴
，
即N点坐标为
．
由N点在椭圆上，则
即5k4－2k2－3＝0．∴k2＝1或k2＝－
（舍）．
故存在k＝±1使
（2）
＝x1x2＋k2（x1－m）（x2－m）
＝（1＋k2）x1x2－k2m（x1＋x2）＋k2m2
＝（1＋k2）·
由
得
即k2－15≤－20k2－12, k2≤
且k≠0．
练习册系列答案
备战中考寒假系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
