题目内容
已知函数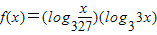
(1)若
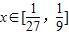 ,求函数f(x)最大值和最小值;
,求函数f(x)最大值和最小值;(2)若方程f(x)+m=0有两根α,β,试求α•β的值.
【答案】分析:(1)将f(x)计算化简得出f(x)=(log3x-3)(log3x+1),令log3x=t,转化为二次函数解决.
(2)结合(1)即为方程(log3x)2-2log3x-3+m=0的两解为α,β,得出log3α+log3β=2,再求出α•β.
解答:解:(1)根据对数的运算性质得出
f(x)=(log3x-3)(log3x+1)
令log3x=t,t∈[-3,-2]
则g(t)=t2-2t-3,t∈[-3,-2]
g(t)对称轴t=1
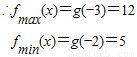
(2)即方程(log3x)2-2log3x-3+m=0的两解为α,β
∴log3α+log3β=2
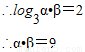
点评:本题考查了二次函数的性质,根与系数的关系,对数的运算等知识,换元的思想方法.
(2)结合(1)即为方程(log3x)2-2log3x-3+m=0的两解为α,β,得出log3α+log3β=2,再求出α•β.
解答:解:(1)根据对数的运算性质得出
f(x)=(log3x-3)(log3x+1)
令log3x=t,t∈[-3,-2]
则g(t)=t2-2t-3,t∈[-3,-2]
g(t)对称轴t=1
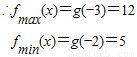
(2)即方程(log3x)2-2log3x-3+m=0的两解为α,β
∴log3α+log3β=2
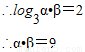
点评:本题考查了二次函数的性质,根与系数的关系,对数的运算等知识,换元的思想方法.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目

 ,求在
,求在 图象与
图象与 轴交点处的切线方程;
轴交点处的切线方程; 的范围.
的范围.
 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 在其定义域内为增函数,求
在其定义域内为增函数,求 的取值范围;
的取值范围; ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得

 成立,求实数
成立,求实数
 ,求实数
,求实数 的取值范围;
的取值范围; 在区间[1,2]上恒成立,求实数
在区间[1,2]上恒成立,求实数 的取值范围.
的取值范围. .
. ,求
,求 的值;
的值; 对于
对于 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。