题目内容
已知椭圆 的右焦点为F,下顶点为A,直线AF与椭圆的另一交点为B,点B关于x轴的对称点为C,若四边形OACB为平行四边形(O为坐标原点),则椭圆的离心率等于
的右焦点为F,下顶点为A,直线AF与椭圆的另一交点为B,点B关于x轴的对称点为C,若四边形OACB为平行四边形(O为坐标原点),则椭圆的离心率等于
- A.

- B.

- C.

- D.

C
分析:由已知中椭圆 的右焦点为F,下顶点为A,直线AF与椭圆的另一交点为B,点B关于x轴的对称点为C,若四边形OACB为平行四边形,根据平行四边形的性质,我们易求出B点的坐标,然后根据A,F,B三点共线,即可求出椭圆的离心率.
的右焦点为F,下顶点为A,直线AF与椭圆的另一交点为B,点B关于x轴的对称点为C,若四边形OACB为平行四边形,根据平行四边形的性质,我们易求出B点的坐标,然后根据A,F,B三点共线,即可求出椭圆的离心率.
解答:∵椭圆 的右焦点为F,下顶点为A,
的右焦点为F,下顶点为A,
直线AF与椭圆的另一交点为B,点B关于x轴的对称点为C,
若四边形OACB为平行四边形
则OA=BC=b
则B点的纵坐标为
B点的横坐标为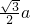
即(0,-b),(c,0),(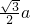 ,
, ) 三点共线
) 三点共线
则c= a
a
则e=
故选C.
点评:本题的考查的知识点是椭圆的简单性质,其中根据平行四边形的性质,求出B点的坐标,是解答本题的关键.
分析:由已知中椭圆
 的右焦点为F,下顶点为A,直线AF与椭圆的另一交点为B,点B关于x轴的对称点为C,若四边形OACB为平行四边形,根据平行四边形的性质,我们易求出B点的坐标,然后根据A,F,B三点共线,即可求出椭圆的离心率.
的右焦点为F,下顶点为A,直线AF与椭圆的另一交点为B,点B关于x轴的对称点为C,若四边形OACB为平行四边形,根据平行四边形的性质,我们易求出B点的坐标,然后根据A,F,B三点共线,即可求出椭圆的离心率.解答:∵椭圆
 的右焦点为F,下顶点为A,
的右焦点为F,下顶点为A,直线AF与椭圆的另一交点为B,点B关于x轴的对称点为C,
若四边形OACB为平行四边形
则OA=BC=b
则B点的纵坐标为

B点的横坐标为
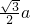
即(0,-b),(c,0),(
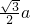 ,
, ) 三点共线
) 三点共线则c=
 a
a则e=

故选C.
点评:本题的考查的知识点是椭圆的简单性质,其中根据平行四边形的性质,求出B点的坐标,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.  ,试用
,试用 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C