题目内容
(2007
上海春,17)求出一个数学问题的正确结论后,将其作为条件之一,提出与原来问题有关的新问题,我们把它称为原来问题的一个“逆向”问题.例如,原来问题是“若正四棱锥底面边长为
4,侧棱长为3,求该正四棱锥的体积”.求出体积 后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为
后,它的一个“逆向”问题可以是“若正四棱锥底面边长为4,体积为 ,求侧棱长”;也可以是“若正四棱锥的体积为
,求侧棱长”;也可以是“若正四棱锥的体积为 ,求所有侧面面积之和的最小值”.
,求所有侧面面积之和的最小值”.
试给出问题“在平面直角坐标系
xOy中,求点P(2,1)到直线3x+4y=0的距离”的一个有意义的“逆向”问题,并解答你所给出的“逆向”问题.
答案:略
解析:
提示:
解析:
|
解析:点 (2,1)到直线3x+4y=0的距离为
“逆向”问题可以是 (1) 求到直线3x+4y=0的距离为2的点的轨迹方程. 10分解:设所求轨迹上任意一点为 P(x,y),则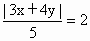 , ,
所求轨迹为3x+4y-10=0或3x+4y+10=0 14分 (2) 若点P(2,1)到直线l∶ax+by=0的距离为2,求直线l的方程.10分解: 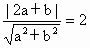 ,化简得 ,化简得 ,b=0或4a=3b, ,b=0或4a=3b,
所以,直线l的方程为x=0或3x+4y=0. 14分 意义不大的“逆向”问题可能是 (3) 点P(2,1)是不是到直线3x+4y=0的距离为2的一个点? 6分解:因为 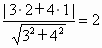 , ,
所以点P(2,1)是到直线3x+4y=0的距离为2的一个点. 10分 (4) 点Q(1,1)是不是到直线3x+4y=0的距离为2的一个点? 6分解:因为 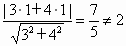 , ,
所以点 Q(1,1)不是到直线3x+4y=0的距离为2的一个点. 10分(5) 点P(2,1)是不是到直线5x+12y=0的距离为2的一个点? 6分解:因为 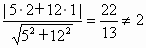 , ,
所以点 P(2,1)不是到直线5x+12y=0的距离为2的一个点. |
提示:
|
剖析:本题考查点到直线的距离公式,考查综合能力及创新意识. |

练习册系列答案
相关题目

 ;
;


