题目内容
已知集合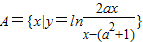 ,B={x|(x-2)(x-3a-1)<0}.
,B={x|(x-2)(x-3a-1)<0}.(1)若a=2,求集合A;
(2)若B⊆A,求实数a的取值范围.
【答案】分析:(1)把a=2代入集合A,根据对数函数的性质,可得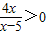 ,从而求出集合A;
,从而求出集合A;
(2)因为B⊆A,可以解出集合B,根据子集的性质,讨论集合B为空集的情况,从而进行求解;
解答:解:(1)集合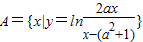 ,把a=2代入A,根据对数函数的性质,
,把a=2代入A,根据对数函数的性质,
可得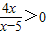 得集合A=(-∞,0)∪(5,+∞);
得集合A=(-∞,0)∪(5,+∞);
(2)当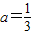 时,B=∅⊆A,符合题意,
时,B=∅⊆A,符合题意,
当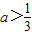 时,有B=(2,3a+1),A=(-∞,0)∪(a2+1,+∞),由B⊆A得a2+1≤2,所以
时,有B=(2,3a+1),A=(-∞,0)∪(a2+1,+∞),由B⊆A得a2+1≤2,所以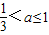 ,
,
当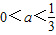 时,有B=(3a+1,2),A=(-∞,0)∪(a2+1,+∞),由B⊆A得a2+1≤3a+1,所以
时,有B=(3a+1,2),A=(-∞,0)∪(a2+1,+∞),由B⊆A得a2+1≤3a+1,所以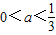 ,
,
当a=0时,不合题意,舍去,
当a<0时,有B=(3a+1,2),A=(0,a2+1),
由B⊆A得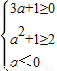 ,无解,
,无解,
综上,实数a的取值范围是(0,1].
点评:此题主要考查对数函数的定义域,以及子集的性质,是一道基础题,解题过程中用到了分类讨论的思想;
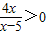 ,从而求出集合A;
,从而求出集合A;(2)因为B⊆A,可以解出集合B,根据子集的性质,讨论集合B为空集的情况,从而进行求解;
解答:解:(1)集合
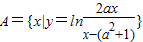 ,把a=2代入A,根据对数函数的性质,
,把a=2代入A,根据对数函数的性质,可得
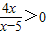 得集合A=(-∞,0)∪(5,+∞);
得集合A=(-∞,0)∪(5,+∞);(2)当
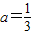 时,B=∅⊆A,符合题意,
时,B=∅⊆A,符合题意,当
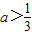 时,有B=(2,3a+1),A=(-∞,0)∪(a2+1,+∞),由B⊆A得a2+1≤2,所以
时,有B=(2,3a+1),A=(-∞,0)∪(a2+1,+∞),由B⊆A得a2+1≤2,所以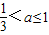 ,
,当
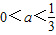 时,有B=(3a+1,2),A=(-∞,0)∪(a2+1,+∞),由B⊆A得a2+1≤3a+1,所以
时,有B=(3a+1,2),A=(-∞,0)∪(a2+1,+∞),由B⊆A得a2+1≤3a+1,所以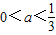 ,
,当a=0时,不合题意,舍去,
当a<0时,有B=(3a+1,2),A=(0,a2+1),
由B⊆A得
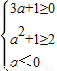 ,无解,
,无解,综上,实数a的取值范围是(0,1].
点评:此题主要考查对数函数的定义域,以及子集的性质,是一道基础题,解题过程中用到了分类讨论的思想;

练习册系列答案
相关题目
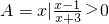 ,B={x|(x+3)(x-a2)≤0}.
,B={x|(x+3)(x-a2)≤0}.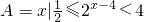 ,B={x|x2-11x+18<0}.
,B={x|x2-11x+18<0}. ,B={x|x2-11x+18<0}.
,B={x|x2-11x+18<0}. ,B={x|(x+a)(x-2a)≤0},其中a>0.
,B={x|(x+a)(x-2a)≤0},其中a>0. ,B={x|m+1≤x≤3m-1}.
,B={x|m+1≤x≤3m-1}.