Question

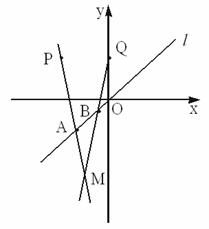
已知两点P（-2，2）、Q（0，2），以及一条直线y=x，设长为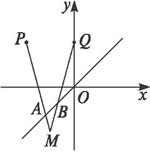的线段AB在直线上运动，如图，求直线PA和QB的交点M的轨迹方程，说明轨迹是什么曲线.

Answer 1

思路解析：由于动点M在PA与QB的交点上，故考虑交轨迹比较方便.

解：∵A、B均在直线y=x上，设A（x₀,x₀）,

又线段|AB|=，则B（x₀+1,x₀+1）.

PA的方程为=,

QB的方程为=.

∵M是直线PA和QB的交点，

∴M点的轨迹方程为

消去参数x₀，得x²-y²+2x-2y-8=0,

即是-=1,它是中心在（-1，-1）的等轴双曲线.