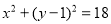题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x≤4}\\{f(x-1),x>4}\end{array}\right.$,求f(8-log23)的值.分析 利用分段函数求解函数值即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x≤4}\\{f(x-1),x>4}\end{array}\right.$,8-log23∈(6,7).
f(8-log23)=f(7-log23)=f(6-log23)=f(5-log23)=${2}^{-5+{log}_{2}3}$=$\frac{3}{32}$.
点评 本题考查分段函数的应用,函数的值的求法,考查计算能力.

练习册系列答案
相关题目
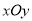 中,点
中,点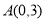 ,直线
,直线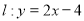 ,设圆
,设圆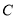 的半径为
的半径为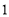 ,圆心在
,圆心在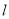 上.
上.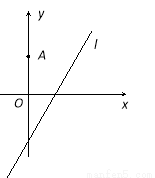
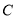 也在直线
也在直线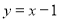 上,过点
上,过点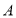 作圆
作圆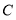 的切线,求切线的方程;
的切线,求切线的方程;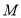 ,使
,使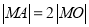 ,求圆心
,求圆心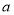 的取值范围.
的取值范围.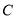 的圆心与点
的圆心与点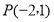 关于直线
关于直线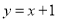 对称.直线
对称.直线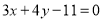 与圆
与圆 相交于
相交于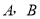 两点,且
两点,且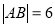 ,则圆
,则圆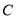 的方程为
的方程为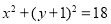 B.
B.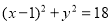
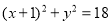 D.
D.