题目内容
已知动圆C与圆(x+1)2+y2=1及圆(x-1)2+y2=25都内切,则动圆圆心C的轨迹方程为 .
分析:设圆(x+1)2+y2=1的圆心O1(-1,0),半径r1=1;圆(x-1)2+y2=25的圆心O2(1,0),半径r2=5.设动圆C的圆心C(x,y),半径R.由于动圆C与圆(x+1)2+y2=1及圆(x-1)2+y2=25都内切,可得|O1C|=R-1,|O2C|=5-R.于是|O1C|+|O2C|=5-1=4>|O1O2|=2,利用椭圆的定义可知:动点C的轨迹是椭圆.求出即可.
解答:解:设圆(x+1)2+y2=1的圆心O1(-1,0),半径r1=1;圆(x-1)2+y2=25的圆心O2(1,0),半径r2=5.
设动圆C的圆心C(x,y),半径R.
∵动圆C与圆(x+1)2+y2=1及圆(x-1)2+y2=25都内切,
∴|O1C|=R-1,|O2C|=5-R.
∴|O1C|+|O2C|=5-1=4>|O1O2|=2,
因此动点C的轨迹是椭圆,设其标准方程为:
+
=1.
则2a=4,2c=2,解得a=2,c=1,∴b2=a2-c2=3.
因此动圆圆心C的轨迹方程是
+
=1.
故答案为:
+
=1.
设动圆C的圆心C(x,y),半径R.
∵动圆C与圆(x+1)2+y2=1及圆(x-1)2+y2=25都内切,
∴|O1C|=R-1,|O2C|=5-R.
∴|O1C|+|O2C|=5-1=4>|O1O2|=2,
因此动点C的轨迹是椭圆,设其标准方程为:
| x2 |
| a2 |
| y2 |
| b2 |
则2a=4,2c=2,解得a=2,c=1,∴b2=a2-c2=3.
因此动圆圆心C的轨迹方程是
| x2 |
| 4 |
| y2 |
| 3 |
故答案为:
| x2 |
| 4 |
| y2 |
| 3 |
点评:本题考查了两圆相内切的性质、椭圆的定义,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
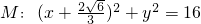 相切,且经过点
相切,且经过点 .
. ,请求出实数t的值;
,请求出实数t的值; ,点T是曲线C上的动点,试求
,点T是曲线C上的动点,试求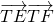 的最小值.
的最小值.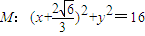 相切,且经过点
相切,且经过点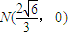 .
.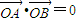 ,请求出实数t的值;
,请求出实数t的值;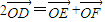 ,点T是曲线C上的动点,试求
,点T是曲线C上的动点,试求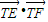 的最小值.
的最小值.