题目内容
已知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比,
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列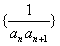 的前n项和,若λTn≤an+1对一切n∈N*恒成立,求实数λ的最大值。
的前n项和,若λTn≤an+1对一切n∈N*恒成立,求实数λ的最大值。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列
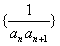 的前n项和,若λTn≤an+1对一切n∈N*恒成立,求实数λ的最大值。
的前n项和,若λTn≤an+1对一切n∈N*恒成立,求实数λ的最大值。解:(Ⅰ)设公差为d,
由已知得 ,
,
联立解得d=1或d=0(舍去),
∴a1=2,故an=n+1;
(Ⅱ) ,
,
∴ ,
,
∵λTn≤an+1,
∴ ,
,
∴ ,
,
又 ,
,
∴λ的最大值为12。
由已知得
 ,
,联立解得d=1或d=0(舍去),
∴a1=2,故an=n+1;
(Ⅱ)
 ,
, ∴
 ,
,∵λTn≤an+1,
∴
 ,
, ∴
 ,
,又
 ,
, ∴λ的最大值为12。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 的前四项和
的前四项和 ,且
,且 成等比.
成等比. 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值. 的前四项和
的前四项和 ,且
,且 成等比.
成等比. 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.