Question

【题目】(本小题满分12分)

已知=12sin(x+)cosx-3,x∈[o,].

(1)求的最大值、最小值;

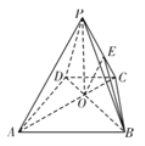
(Ⅱ)CD为△ABC的内角平分线,已知AC=max,BC=,CD=2,求∠C.

Answer 1

【答案】( Ⅰ) max =6 , min =3.

( Ⅱ ) C=.

【解析】分析：第一问先对函数解析式进行化简，首先应用正弦的和角公式拆，之后应用正余弦的倍角公式降次升角，之后应用辅助角公式化简，之后将整体角的取值范围求出，再判断其最值，第二问先将第一问求的结果代入，之后借助于正余弦定理找出对应的量，求得结果.

详解：( Ⅰ ) =6sin ( 2 x + )

∵ 在( 0 ,)上单调递增,( )上单调递减

∴ max =6 , min =3

( Ⅱ )在 ΔADC 中,=,在 ΔBDC中,=

∵sin∠ADC=sin∠ BDC , AC=6 , BC =3

∴ AD=2BD 在ΔBCD中, BD2 =17-12cos,

在ΔACD中, AD2=44-24cos=68-48cos

∴cos=,即 C=( Ⅰ) max =6 , min =3.

( Ⅱ ) C=.