题目内容
如图所示,在四面体ABCD中,E、F分别是BC、DA的中点.若AC=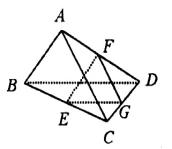
答案:
解析:
解析:
| 取CD的中点G连结EG、FG,则EG∥BD,FG∥AC,故∠ECF(或其补角)为异面直线AC与BD所成的角.
∵AC=2,BD=4 ∴FG=1,EG=2 在△EGF中,由余弦定理,得cos∠EGF= ∴∠EGF=60°,即AC与BD所成的角为60°. |

练习册系列答案
相关题目
 如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.
如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.


 如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.
如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.