Question

已知：函数f(x)=|log2x|-(

1

2

)x有两个零点x₁，x₂，则有（　　）

A．x₁x₂＜0

B．0＜x₁x₂＜1

C．x₁x₂=1

D．x₁x₂＞1

Answer 1

分析：本题数形结合比较容易看出两个零点的位置，考察函数零点，借助于对数性质综合解决．

解答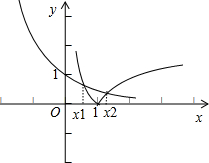：解：∵f（x）=|lgx|-（

1

2

）x有两个零点x₁，x₂，即y=|lgx|与y=2^-x的图象有两个交点，
由题意x＞0，分别画y=2^-x和y=|lgx|的图象，发现在（0，1）和（1，+∞）有两个交点．
不妨设 x₁在（0，1）里，x₂在（1，+∞）里，
那么在（0，1）上有 ^_2-x1 =-lg（x₁），即-2-x1=lgx₁，…①
在（2，+∞）有2 ^-x₂ =lg x₂ ，…②
①、②相加有 2^-x₂ -2^-x₁=lg x₁x₂，
∵x₂＞x₁，∴-x₂＞＜-x₁，∴2^-x₂＜2^-x₁，即 2^-x₂ -2^-x₁＜0．
∴lgx₁x₂＜0，∴0＜x₁x₂＜1，
故选A．

点评：本题主要考查确定函数零点所在区间的方法--转化为两个函数的交点问题．函数的零点等价于函数与x轴的交点的横坐标，借助于图象和性质比较简单，属于基础题．