题目内容
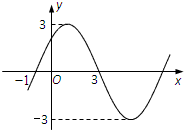已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，φ∈[0，π））的图象如图所示．（1）求f（x）的解析式；
（2）求函数g（x）=f（x）+
| 3 |
分析：（1）由图易知A=3，T=8，f（1）=3，从而可求ω及φ；
（2）由（1）知f（x）=3sin（
x+
），于是可求g（x）=f（x）+
f（x+2）=6sin（
x+
）．当x∈[-1，3]⇒
x+
∈[
，
]，利用正弦函数的单调性即可求得
g（x）在x∈[-1，3]上的最大值和最小值．
（2）由（1）知f（x）=3sin（
| π |
| 4 |
| π |
| 4 |
| 3 |
| π |
| 4 |
| 7π |
| 12 |
| π |
| 4 |
| 7π |
| 12 |
| π |
| 3 |
| 4π |
| 3 |
g（x）在x∈[-1，3]上的最大值和最小值．
解答：解：（1）由图可得A=3，
f（x）的周期为8，则
=4，即ω=
；
f（-1）=f（3）=0，则f（1）=3，
∴sin（
+φ）=1，即
+φ=
+2kπ，k∈Z，又φ∈[0，π），
∴φ=
，
综上所述，f（x）的解析式为f（x）=3sin（
x+
）；
（2）g（x）=f（x）+
f（x+2）
=3sin（
x+
）+3
sin[
（x+2）+
）]
=3sin（
x+
）+3
cos（
x+
）
=6[
sin（
x+
）+
cos（
x+
）]
=6sin（
x+
）．
当x∈[-1，3]时，
x+
∈[
，
]，
故当
x+
=
即x=-
时，sin（
x+
）取得最大值为1，
则g（x）的最大值为g（-
）=6；
当
x+
=
即x=3时，sin（
x+
）取得最小值为-
，
则g（x）的最小值为g（3）=6×（-
）=-3
．
f（x）的周期为8，则
| 2π |
| ω |
| π |
| 4 |
f（-1）=f（3）=0，则f（1）=3，
∴sin（
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴φ=
| π |
| 4 |
综上所述，f（x）的解析式为f（x）=3sin（
| π |
| 4 |
| π |
| 4 |
（2）g（x）=f（x）+
| 3 |
=3sin（
| π |
| 4 |
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
=3sin（
| π |
| 4 |
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
=6[
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
=6sin（
| π |
| 4 |
| 7π |
| 12 |
当x∈[-1，3]时，
| π |
| 4 |
| 7π |
| 12 |
| π |
| 3 |
| 4π |
| 3 |
故当
| π |
| 4 |
| 7π |
| 12 |
| π |
| 2 |
| 1 |
| 3 |
| π |
| 4 |
| 7π |
| 12 |
则g（x）的最大值为g（-
| 1 |
| 3 |
当
| π |
| 4 |
| 7π |
| 12 |
| 4π |
| 3 |
| π |
| 4 |
| 7π |
| 12 |
| ||
| 2 |
则g（x）的最小值为g（3）=6×（-
| ||
| 2 |
| 3 |
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查三角函数变换与正弦函数的单调性与最值的综合应用，属于难题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目