Question

（本小题满分12分）已知数列的各项均为正数，且满足.

(1)求数列的通项公式；

（2）求证：对任意的都成立。

Answer 1

解：（1）

                    _{……………2分}

                 _{……………6分}

（2）_{………8分}

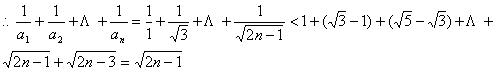
_{…………………10分}

  _{……………………………………………12分}

方法二：数学归纳法

当n=1时，左边=1，右边=1，不等式成立。   _{…………………………………7分}

假设n=k结论成立，即：

   _{……………………………8分}

那么当n=k+1时，

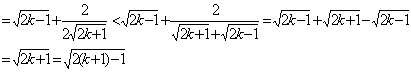
所以当n=k+1时，结论成立。         _{…………………………………………………11分}

综合以上（1）（2）不等式对于任意的成立。     _{……………………………12分}

_{（其它证法以例给分）}