题目内容
△ABC的三个顶点分别是A(1,-1,2),B(5,-6,2),C(1,3,-1),则AC边上的高BD长为______.
∵A(1,-1,2),B(5,-6,2),C(1,3,-1),
∴
=(4,-5,0),
=(0,4,-3),
∵点D在直线AC上,
∴设
=λ
=(0,4λ,-3λ),
由此可得
=
-
=(0,4λ,-3λ)-(4,-5,0)=(-4,4λ+5,-3λ),
又∵
⊥
,
∴
•
=-4×0+(4λ+5)×4+(-3λ)×(-3)=0,解得λ=-
.
因此
=(-4,4λ+5,-3λ)=(-4,
,
),
可得|
|=
=5
故答案为:5
∴
| AB |
| AC |
∵点D在直线AC上,
∴设
| AD |
| AC |
由此可得
| BD |
| AD |
| AB |
又∵
| BD |
| AC |
∴
| BD |
| AC |
| 4 |
| 5 |
因此
| BD |
| 9 |
| 5 |
| 12 |
| 5 |
可得|
| BD |
(-4)2+(
|
故答案为:5

练习册系列答案
相关题目
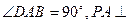 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=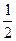 AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。
AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。
 是两条异面直线,
是两条异面直线,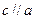 ,那么
,那么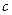 与
与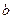 的位置关系____________________。
的位置关系____________________。