题目内容
6.等差数列{an}的前n项和为Sn,若当首项a1和公差d变化时,a3+a10+a11是一个定值,则下列选项中为定值的是( )| A. | S17 | B. | S16 | C. | S15 | D. | S14 |
分析 由题意和等差数列的性质可得a8为定值,又可得S15=15a8,可得结论.
解答 解:由题意可得a3+a10+a11=(a1+2d)+(a1+9d)+(a1+10d)
=3a1+21d=3(a1+7d)=3a8为定值,即a8为定值,
∴由等差数列的求和公式和性质可得S15=$\frac{15({a}_{1}+{a}_{15})}{2}$=$\frac{15×2{a}_{8}}{2}$=15a8为定值.
故选:C.
点评 本题考查等差数列的求和公式和等差数列的性质,转化为a8是解决问题的关键,属基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17.已知(x${\;}^{lo{g}_{2}x}$+1)n展开式中有连续三项之比为1:2:3,且展开式的倒数第二项为28,则x的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | $\frac{1}{2}$或2 |
14.设集合M={0,1,2,3},P={2,3,4},那么“x∈M或x∈P”是“x∈M∩P”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.圆C:x2+y2-14x+10y+65=0的面积等于( )
| A. | π | B. | 3π | C. | 6π | D. | 9π |
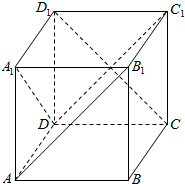
 一个四棱锥的三视图如图所示,则该几何体的体积=$\frac{2}{3}$,表面积=2+$\sqrt{2}$+$\sqrt{6}$.
一个四棱锥的三视图如图所示,则该几何体的体积=$\frac{2}{3}$,表面积=2+$\sqrt{2}$+$\sqrt{6}$.