题目内容
在正方体ABCD—A1B1C1D1中，E、F分别是BB1、D1B1的中点.求证：EF⊥平面B1AC.
证明：设正方体的棱长为2,取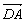
、
、
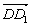的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系如图，则?
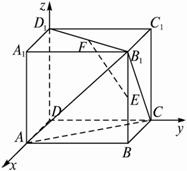
A（2，0，0）、C（0，2，0）、B1（2，2，2）、E（2，2，1）、F（1，1，2）.?
∴
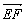=(1,1,2)-(2,2,1)=(-1,-1,1),?
=(2,2,2)-(2,0,0)=(0,2,2),?
=(0,2,0)-(2,0,0)=(-2,2,0).?
∵
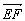·=（-1，-1，1）·（0，2，2）=（-1）×0+（-1）×2+1×2=0，?
·
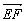=（-1，-1，1）·（-2，2，0）=2-2+0=0，?
∴EF⊥AB1，EF⊥AC.?
又AB1∩AC=A,?
∴EF⊥平面B1AC.
点评:用向量的坐标运算证明向量垂直的关键在于建立适当的坐标系并且正确的求出各点及相关向量的坐标.
练习册系列答案
53随堂测系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）