题目内容
在三角形中,对任意λ都有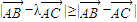 ,则△ABC形状( )
,则△ABC形状( )A.锐角三角形
B.钝角三角形
C.直角三角形
D.等腰三角形
【答案】分析:在三角形ABC中,A,B,C的对边分别为a,b,c,将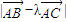 ≥
≥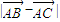 ?
?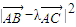 ≥
≥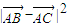 ?c2+λ2b2-2bcλcosA≥a2,整理成关于λ的二次不等式恒成立问题,利用△≤0结合正弦定理可得到sin2C≥1,从而可得答案.
?c2+λ2b2-2bcλcosA≥a2,整理成关于λ的二次不等式恒成立问题,利用△≤0结合正弦定理可得到sin2C≥1,从而可得答案.
解答:解:在△ABC中,设A,B,C的对边分别为a,b,c,则 =c,
=c,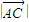 =b,
=b,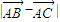 =
=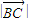 =a,
=a,
∵对任意λ都有 ≥
≥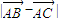 ,
,
∴对任意λ都有 ≥
≥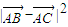 ,
,
即c2+λ2b2-2bcλcosA≥a2对任意λ恒成立,
即λ2b2-2bccosA•λ+c2-a2≥0恒成立,
∵b2>0,
∴△=4b2c2cos2A-4b2(c2-a2)≤0,
∴c2sin2A≥a2,
在三角形ABC中,由正弦定理可得sin2Csin2A≥sin2A,
∴sin2C≥1,又C为△ABC的内角,0<sinC≤1,
∴sinC=1.
∴三角形ABC为直角三角形.
故选C.
点评:本题考查三角形的形状判断,考查向量的数量积,考查二次不等式恒成立问题,考查正弦定理,考查分析转化与综合应用、解决问题的能力,属于难题.
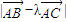 ≥
≥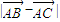 ?
?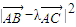 ≥
≥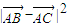 ?c2+λ2b2-2bcλcosA≥a2,整理成关于λ的二次不等式恒成立问题,利用△≤0结合正弦定理可得到sin2C≥1,从而可得答案.
?c2+λ2b2-2bcλcosA≥a2,整理成关于λ的二次不等式恒成立问题,利用△≤0结合正弦定理可得到sin2C≥1,从而可得答案.解答:解:在△ABC中,设A,B,C的对边分别为a,b,c,则
 =c,
=c,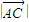 =b,
=b,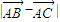 =
=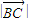 =a,
=a,∵对任意λ都有
 ≥
≥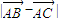 ,
,∴对任意λ都有
 ≥
≥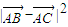 ,
,即c2+λ2b2-2bcλcosA≥a2对任意λ恒成立,
即λ2b2-2bccosA•λ+c2-a2≥0恒成立,
∵b2>0,
∴△=4b2c2cos2A-4b2(c2-a2)≤0,
∴c2sin2A≥a2,
在三角形ABC中,由正弦定理可得sin2Csin2A≥sin2A,
∴sin2C≥1,又C为△ABC的内角,0<sinC≤1,
∴sinC=1.
∴三角形ABC为直角三角形.
故选C.
点评:本题考查三角形的形状判断,考查向量的数量积,考查二次不等式恒成立问题,考查正弦定理,考查分析转化与综合应用、解决问题的能力,属于难题.

练习册系列答案
相关题目
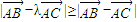 ,则△ABC形状( )
,则△ABC形状( )