题目内容
直线l：y=k（x-2）+2将圆C：x2+y2-2x-2y=0平分，则直线l的方向向量是
- A.（2，-2）
- B.（2，2）
- C.（-3，2）
- D.（2，1）
B
分析：利用圆心C（1，1）在直线l上求出k，从而得到直线方程，进而得到直线的法向量的和方向向量．
解答：∵圆C：x2+y2-2x-2y=0 的圆心C（1，1），直线l：y=k（x-2）+2将圆C：x2+y2-2x-2y=0平分，
故圆心C（1，1）在直线l上，
∴1=k（1-2）+2，∴k=1，
故直线l的方程为x-y-2=0，其法向量为（1，-1），
故直线l的方向向量与（1，1）平行，
故选B．
点评：本题考查直线和圆相交的性质，直线的方向向量和法向量的定义，关键是判断圆心C在直线l上．
分析：利用圆心C（1，1）在直线l上求出k，从而得到直线方程，进而得到直线的法向量的和方向向量．
解答：∵圆C：x2+y2-2x-2y=0 的圆心C（1，1），直线l：y=k（x-2）+2将圆C：x2+y2-2x-2y=0平分，
故圆心C（1，1）在直线l上，
∴1=k（1-2）+2，∴k=1，
故直线l的方程为x-y-2=0，其法向量为（1，-1），
故直线l的方向向量与（1，1）平行，
故选B．
点评：本题考查直线和圆相交的性质，直线的方向向量和法向量的定义，关键是判断圆心C在直线l上．
练习册系列答案
名校课堂系列答案
相关题目
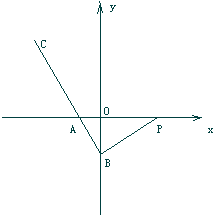如图，已知直角三角形PAB的直角顶点为B，点P的坐标为（3，0），点B在y轴上，点A在x轴的负半轴上，在BA的延长线上取一点C，使