题目内容
【题目】在直角坐标系![]() 中,已知定点
中,已知定点![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() ,设点
,设点![]() 的曲线为
的曲线为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点.
两点.![]()
(1)写出曲线![]() 的方程,并指出曲线
的方程,并指出曲线![]() 的轨迹;
的轨迹;
(2)当![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)证明:存在直线![]() ,满足
,满足![]() ,并求实数
,并求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,曲线
,曲线![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的双曲线的上支;(2)
为焦点的双曲线的上支;(2)![]() 或
或![]() ;(3)详见解析,
;(3)详见解析,![]() ,
,![]()
【解析】
(1)结合双曲线的定义,可知点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的双曲线的上支,求出轨迹方程即可;
为焦点的双曲线的上支,求出轨迹方程即可;
(2)将直线与![]() 的方程联立,消去
的方程联立,消去![]() ,可得到关于
,可得到关于![]() 的一元二次方程,令
的一元二次方程,令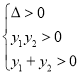 ,求解即可;
,求解即可;
(3)联立直线与![]() 的方程,得到关于
的方程,得到关于![]() 的一元二次方程,由
的一元二次方程,由![]() ,可得
,可得![]() ,设
,设![]() ,则
,则![]() ,结合根与系数关系,可得到
,结合根与系数关系,可得到![]() ,若存在符合题意的直线,还需要满足以下三个条件:①
,若存在符合题意的直线,还需要满足以下三个条件:①![]() ;②
;②![]() ;③
;③![]() ,求解即可.
,求解即可.
(1)动点![]() 满足
满足![]() ,且
,且![]() 、
、![]() ,所以点
,所以点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的双曲线的上支,
为焦点的双曲线的上支,![]() ,
,![]() ,
,![]() ,
,
所以曲线![]() 的方程为
的方程为![]() ;
;
(2)由题意,联立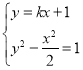 ,消去
,消去![]() ,得
,得![]() ,
,
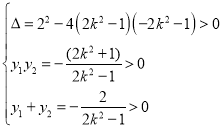 ,解得
,解得![]() 或
或![]() .
.
故![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
(3)因为![]() ,所以
,所以![]() ,设
,设![]() ,则
,则![]() .
.
联立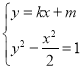 ,可得
,可得![]() ,
,![]() ,
,
则![]()
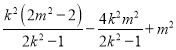
![]() ,
,![]() ,
,
所以![]() ,整理得
,整理得![]() .
.
若存在符合题意的直线,还需要满足以下三个条件:①![]() ;②
;②![]() ;③
;③![]() .
.
①![]() ,整理得
,整理得![]() ,又
,又![]() ,则
,则![]() ,显然恒成立;
,显然恒成立;
②![]() ,等价于
,等价于![]() ,
,
因为![]() 恒成立,所以
恒成立,所以![]() ,即
,即![]() ;
;
③![]() ,由②知
,由②知![]() ,所以
,所以![]() .
.
所以![]() 满足
满足![]() ,即
,即![]() .
.
又因为![]() ,所以
,所以![]() ,且
,且![]() ,故
,故![]() .
.
所以存在直线![]() ,满足
,满足![]() ,
,![]() 的取值范围为:
的取值范围为:![]() ,
,![]() 的取值范围为:
的取值范围为:![]() .
.

练习册系列答案
相关题目